前言
本文章为自用笔记，部分图片和部分内容版权归原出处所有。
原网课链接为：GAMES101-现代计算机图形学入门-闫令琪。
笔记可能存在纰漏，欢迎在评论区指出。
1.线性代数
点乘&叉乘
- 点乘反映向量是否接近（重合正 $\to$ 垂直零 $\to$ 反向负）
叉乘可以反映向量位置关系（顺时针、逆时针）
- 判断点是否在三角形内部（例如用在光栅化）
矩阵
表示线性变换。
叉乘，$A^*$ 为 $\vec{a}$ 的 dual matrix ：
$$ \vec{a}\times\vec{b}=A^*b= \begin{bmatrix} 0&-z_a&y_a\\ z_a&0&-x_a\\ -y_a&x_a&0 \end{bmatrix} \begin{bmatrix} x_b\\ y_b\\ z_b \end{bmatrix} $$
线性变换
构造变换矩阵的方式：找一些参照点写出式子，对应到矩阵参数中。
缩放：$\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}s_x&0\\0&s_y\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$
镜像：例如关于 $y$ 对称 $s_x=-1,s_y=1$
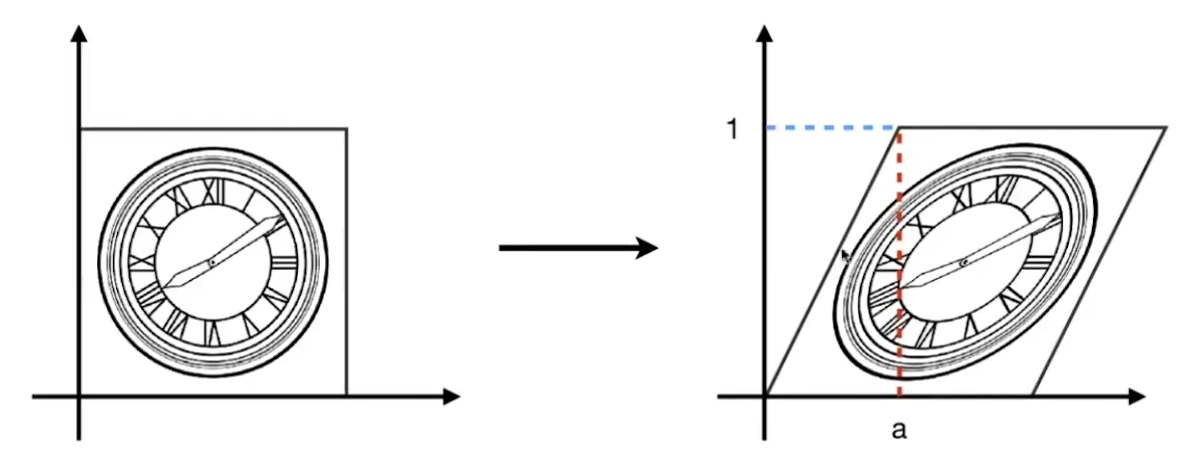
切变：$\begin{bmatrix}x'\\y'\end{bmatrix}=\begin{bmatrix}1&a\\0&1\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$
旋转（绕着原点逆时针旋转 $\theta$ ）：$\begin{bmatrix}x'\\y'\end{bmatrix}=R_\theta\begin{bmatrix}x\\y\end{bmatrix}=\begin{bmatrix}\cos\theta&-\sin\theta\\\sin\theta&\cos\theta\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}$
$R_{-\theta}=\begin{bmatrix}\cos\theta&\sin\theta\\\ -sin\theta&\cos\theta\end{bmatrix}=R_\theta^{T}=R_\theta^{-1}$ ，是正交矩阵
齐次坐标&仿射变换
平移不能直接用坐标进行线性变换（因为有常数）
二维齐次坐标：$(x,y,1)$ ；对应的二维向量改为 $(x,y,0)$
平移：$\begin{bmatrix}x'\\y'\\1\end{bmatrix}=\begin{bmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}=\begin{bmatrix}x+t_x\\y+t_y\\1\end{bmatrix}$
- 向量仍具有平移不变性，向量 $\pm$ 点/向量的含义依然成立
仿射变换：线性变换+平移
单个矩阵时，等价于先线性变换，再平移 $(t_x,t_y)$
- $(x,y,w),w\not=0$ 表示点 $({x\over w},{y\over w})$
- 高维情况同理
组合变换
有 $n$ 种变换矩阵 $\{A_n\}$ 依次对 $\vec{a}$ 执行：$A_nA_{n-1}\cdots A_1\vec{a}$ 。
不符合交换律，但可以任意结合。
*3D旋转和四元数
3D旋转也可以用变换矩阵写出来，比较复杂这里不展示。
除了变换矩阵还可以用四元数表示。
2.变换进阶-观测变换
拍照片：搭好场景（模型 Model 变换），摆相机（视图 View 变换），3D到2D成像（投影 Projection 变换）。
这个过程简称MVP变换，MV变换通常是一起的。
View/Camera 变换（视图/相机变换）
模型空间 $\to$ 世界空间 $\to$ 相机空间。
定义相机位置
- 位置 $\vec{e}$ ，看向（Look-at）方向 $\vec{g}$ ，向上（Up）方向 $\vec{t}$ 。
- 标准位置：通常把相机放在原点，看向方向为 $-Z$ ，向上方向为 $Y$ 。其他点按照相机的移动方式相对移动（模型变换）。
将相机移动到标准位置，使用变换 $M_{view}$
- $M_{view}=R_{view}T_{view}$ ，先位移再旋转
- $T_{view}$ 即表示位移 $(-x_e,-y_e,-z_e)$
$R_{view}$ 表示旋转，将 $\vec{g}$ 转到 $-Z$ ，$t$ 转到 $Y$ ，$\vec{g}\times\vec{t}$ 转到 $X$
先写逆矩阵：$R_{view}^{-1}=\begin{bmatrix}x_{\vec{g}\times\vec{t}}&x_t&x_{-g}&0\\y_{\vec{g}\times\vec{t}}&y_t&y_{-g}&0\\z_{\vec{g}\times\vec{t}}&z_t&z_{-g}&0\\0&0&0&1\end{bmatrix}$ ，代入 $(1,0,0),(0,1,0),(0,0,1)$ 易得
则 $R_{view}=(R_{view}^{-1})^T$（正交矩阵）
Projection 变换（投影变换）
相机空间 $\to$ 裁剪空间。
正交 Orthographic 投影（平行线投影）
框定坐标范围 $[l,r]\times[b,t]\times[f,n]$（左右，下上，远近，右手系往 $-Z$ 看因此远近和 $z$ 大小对应关系是反的），然后映射到 $[-1,1]^3$ 的标准立方体。
先位移 $(-{l+r\over 2},-{b+t\over 2},-{f+n\over 2})$ 然后缩放 $({2\over r-l},{2\over t-b},{2\over n-f})$ 。
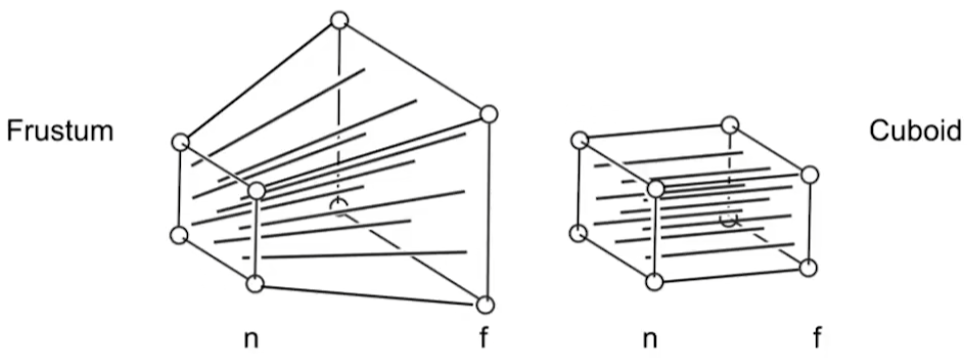
透视 Perspective 投影（点投影，平行线不再平行，近大远小）
从点（相机）往外看，将近 $n$ 和远 $f$ 之间的坐标变换为一个标准长方体，使得近 $n$ 和远 $f$ 的 $z$ 坐标不变，近 $n$ 的平面不变，其他点压缩。
$(x,y,z)\to(x',y',z')$ 根据相似 $x'={n\over z}x,y'={n\over z}y$ 。
由于齐次坐标 $(kx,ky,kz,k),k\not=0$ 表示 $(x,y,z,1)$ ，因此考虑这么构造变换：
$$ M_{p\to o}\begin{bmatrix}x&y&z&1\end{bmatrix}^T=\begin{bmatrix}nx&ny&?&z\end{bmatrix}^T\\ M_{p\to o}=\begin{bmatrix}n&0&0&0\\0&n&0&0\\a&b&c&d\\0&0&1&0\end{bmatrix} $$
根据：1. $n$ 平面不变。2. $f$ 平面 $z$ 坐标不变。构造出矩阵：
$$ \begin{cases} M_{p\to o}\begin{bmatrix}x&y&n&1\end{bmatrix}^T=\begin{bmatrix}nx&ny&n^2&n\end{bmatrix}^T\\ M_{p\to o}\begin{bmatrix}x&y&f&1\end{bmatrix}^T=\begin{bmatrix}nx&ny&f^2&f\end{bmatrix}^T \end{cases} \\ \Rightarrow \begin{cases} ax+by+cn+d=n^2\\ ax+by+cf+d=f^2 \end{cases} \Rightarrow \begin{cases} a=0,b=0\\ cn+d=n^2\\ cf+d=f^2 \end{cases} \Rightarrow \begin{cases} a=0,b=0\\ c=n+f\\ d=-nf \end{cases}\\ M_{p\to o}=\begin{bmatrix}n&0&0&0\\0&n&0&0\\0&0&n+f&-nf\\0&0&1&0\end{bmatrix} $$
变换之后再进行正交投影。
重要性质：用这种方式变换，坐标的第四维 $w$ 就表示原先的深度值。可以用在后续计算上，例如重心坐标的矫正。
课后问题（自己算的，有问题可以评论区指出）：中间点的 $z$ 哪些变小哪些变大。
求变大的（ $0<n<f$ 的情况下）：
$$ {(n+f)z-nf\over z}>z\\ z^2-(n+f)z+nf<0\\ n<z<f $$
所以除了 $n$ 和 $f$ 全都变大了。
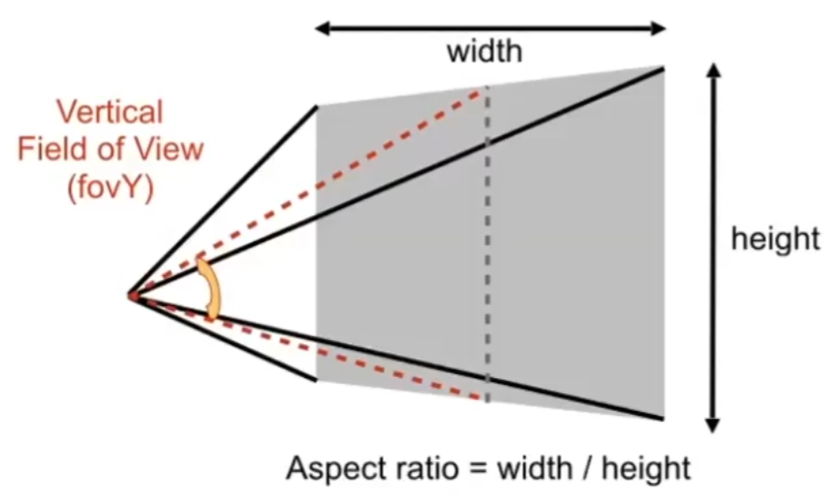
透视投影的视锥
- aspect ratio：近平面的长宽比
- vertical field-of-view (fovY)：近平面的垂直可视角度（上下中点与相机连线的夹角）
定义 $aspect$ 和 $fovY$ 后，可以算出近平面的坐标范围 $[-r,r]\times[-t,t]$ ：
$$ \tan{fovY\over 2}={t\over|n|}\\ aspect={r\over t} $$
3.光栅化
图形学屏幕
二维像素数组，每个像素占据 $1\times 1$ ，空间为 $[0,width]\times[0,height]$ ，长宽为分辨率。
用左下角坐标表示像素，像素中心为 $1\times 1$ 网格中心。
Viewport 变换（视口变换）
裁剪空间 $\to$ 屏幕空间。
先忽略 $z$ 坐标，从正交投影变换到屏幕，即 $[-1,1]^2\to[0,width]\times[0,height]$ 。
$$ M_{vp}=\begin{bmatrix}width\over 2&0&0&width\over 2\\0&height\over 2&0&height\over 2\\0&0&1&0\\0&0&0&1\end{bmatrix} $$
三角形的性质
- 最基础的多边形，多边形都可以拆成三角形。
- 三角形是凸多边形，内外部定义明确。
光栅化 - 采样
采样过程
$inside(tri,x,y)$ 表示 $(x,y)$ 是否在三角形 $tri$ 内部（ $0$ 不在 $1$ 在）。
每个像素用中心对这个函数采样：
image[x][y]=inside(tri,x+0.5,y+0.5)。$inside(tri,x,y)$ 实现方式：用叉乘判断，$(x,y)$ 需要在每条边内侧。
采样优化
- 用一个 Bounding Box 包围三角形，只处理 BB 矩形里面的像素。
- 扫描线，只跑三角形内部的像素。
采样的问题
由于采样是离散的，会出现锯齿等走样的情况。
涉及信号处理知识。
- 采样频率比信号频率低很多的时候就会走样
傅里叶变换：将信号从时域变换为频域
频域上的高频体现出突变（例如二维图像中的轮廓边界）
频域滤波：可以实现锐化（砍低频）、模糊（砍高频，即模糊边界）等操作
- 卷积：时域上的卷积（能转化为频域上的乘积）
光栅化 - 反走样
已知先模糊（即削弱高频），再采样可以反走样（采样频率不变，降信号频率）。
- 理想模糊方法：求出三角形和像素交的面积，根据面积平均涂色（比如交了 $50\%$ 就涂一半颜色），计算量太大了。
- MSAA（Multisample anti-aliasing，多重采样抗锯齿）近似方法：对每个像素再划分网格，用三角形和这些网格求交来近似求出交的面积（但没有增加分辨率即采样率，只是对模糊的一种近似）。
- 还有其他方法例如 FXAA 和 TAA 。
4.着色
画家算法
从远到近画，近的覆盖前面的。
问题：空间中，三角形深度关系可能是成环的（ $A$ 盖 $B$ ，$B$ 盖 $C$ ，$C$ 盖 $A$ ），不能简单地按照三角形顺序来画。
Z-Buffer 深度缓存
对每个像素分析，记录：
- z-buffer 当前最近的深度 $z$ 值
- frame buffer 颜色信息
计算方法：
- 对每个三角形枚举内部的像素 $(x,y)$ ，对应深度 $z$
- 如果 $z$ 比
zbuffer[x,y]小则修正
不需要排序，三角形的执行顺序无关紧要（暂时不考虑三角形有同深度的情况）。
如果用了 MSAA ，深度缓存需要对采样点进行。
处理不了透明物体。
Shading 着色
将不同材质（对光线有不同的作用）应用到物体上。
基础的着色模型（Blinn-Phong 反射模型）对光的表现分为：高光（镜面反射附近）、漫反射、间接光照。
着色是局部的，不会生成阴影（即不考虑其他物体遮挡）。
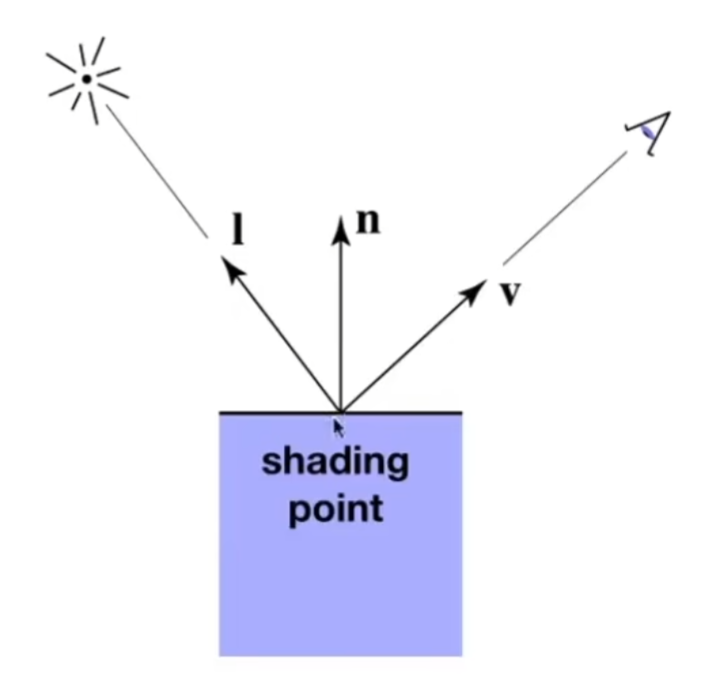
一些定义，方向均为单位向量：1.观察方向 $v$ 。2.表面法线 $n$ 。3.光照方向 $l$（从 shading point 指向光源）。4.表面参数（颜色、光泽度）。
漫反射：光线打到 shading point 上均匀朝四周反射
- 接收：光线被 shading point 接收的能量与夹角余弦值 $\cos\theta=l\cdot n$ 成正比。
- 点光源发射：均匀朝着四面八方发射，球表面上能量守恒，假设距离点光源单位 $1$ 距离处光强为 $I$ ，则 $r$ 处光强为 $I/r^2$ 。
- 漫反射 diffuse 项：结合一下发射和接收，传到 shading point 上的能量为 $L_d=k_d(I/r^2)\max(0,l\cdot n)$ ，$k_d$ 为漫反射系数（产生不同颜色）。当光线成钝角即反向射入的时候没有意义，因此需要和 $0$ 取 $\max$ 。
- 漫反射和观察方向没有关系。
高光：观察方向 $v$ 与镜面反射方向接近的时候才会看到高光
- 转化：等价于法线 $n$ 和 $l,v$ 的半程向量 $h$（角平分线）接近，$\vec{h}={\vec{v}+\vec{l}\over\Vert\vec{v}+\vec{l}\Vert}$ 。
- 衡量接近：用夹角余弦值（的指数）衡量，即 $\cos\alpha=n\cdot h$ 。
- 镜面反射 specular 项：$L_s=k_s(I/r^2)\max(0,n\cdot h)^p$ ，$k_s$ 为镜面反射系数（通常是白色），为了简化不关注接收率（ $l\cdot n$ ）。
- 指数 $p$ 可以降低高光的容忍度，使得离得远的位置值更小（一般 $100$ 到 $200$ ）。
间接光照：虽然有些地方光线照不到，但是从环境中会反射过来
- 大胆的简化：和 $v$ 和 $l$ 都无关，一个常数
- 间接光照 Ambient 项：$L_a=k_aI_a$
- 避免出现完全黑的部分
- Blinn-Phong 反射模型：$L=L_a+L_d+L_s$
Shading Frequencies 着色频率
着色频率
- Flat shading（面）：每个三角形面进行着色，三角形内部结果一致
- Gouraud shading（点）：对每个顶点着色（顶点法线可以插值得出），三角形内部由顶点插值得出
- Phong shading（像素）：对每个像素着色（像素法线用顶点法线再插值得出）
着色频率越来越大，效果越来越好，计算量越来越大。
如果模型本身就足够精细，不一定要用大的着色频率。
计算法线
- 顶点：$N_v={\sum_i N_i\over\Vert \sum_i N_i\Vert}$ ，$\sum_i N_i$ 是顶点 $v$ 所在的所有三角形面的法线之和
- 像素：用重心坐标（详见 5.纹理映射）插值
Real-time Rendering Pipeline 实时渲染管线
模型投影MVP变换 $\to$ 点&三角形 $\to$ 光栅化&深度缓存 $\to$ 着色 $\to$ 帧缓存 $\to$ 像素图像。
GPU已经写好了渲染管线的流程，并支持部分可编程。
Shader 着色器：自定义管线中的部分流程，例如决定顶点、像素如何着色。
5.纹理映射
Texture 纹理
定义着色时不同点的属性，例如 $k_d,k_s$ 。
Texture Map 纹理映射
3D模型表面是2D的。
纹理映射：把3D模型表面的点映射到2D纹理的坐标 $(u,v)$ 上（ $[0,1]\times[0,1]$ ），纹理坐标可以被多次复用。
重心坐标&三角形插值
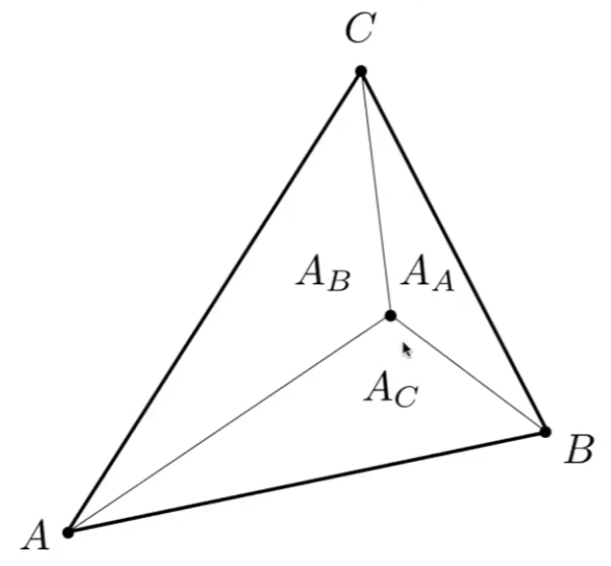
对于 $\triangle ABC$ ，可以定义坐标系 $(\alpha,\beta,\gamma),\alpha+\beta+\gamma =1$ ，表示点 $(x,y)=\alpha A+\beta B+\gamma C$ 。（实际上只有两个参数）
当 $\alpha,\beta,\gamma\ge 0$ 时，$(x,y)$ 在三角形内。
可以通过面积计算（考虑相似易得）：
$\alpha={A_A\over A_A+A_B+A_C},\beta={A_B\over A_A+A_B+A_C},\gamma={A_C\over A_A+A_B+A_C}$
使用重心坐标即可插值：$V=\alpha V_A+\beta V_B+\gamma V_C$ 。插值的内容可以是：位置、颜色、法线、纹理坐标等。
问题：投影之后（2D）重心坐标与原三角形（3D）重心坐标不相同，插值时需要求原三角形的重心坐标。
关于重心坐标的透视投影矫正，可以看这篇。
结论：设 $(x,y)$ 透视投影后的重心坐标是 $(\alpha',\beta',\gamma')$（这个可以直接求出），那么原三角形的重心坐标为 $({Z\over Z_A}\alpha',{Z\over Z_B}\beta',{Z\over Z_C}\gamma')$ ，其中 $Z$ 为投影前的 $(x,y)$ 的深度 $Z$ ，$Z_A,Z_B,Z_C$ 为投影前三角形三个点的深度（可以由齐次坐标第四维 $w$ 得出）。
$$ {Z\over Z_A}\alpha'+{Z\over Z_B}\beta'+{Z\over Z_C}\gamma'=1\Rightarrow {1\over Z}={1\over Z_A}\alpha'+{1\over Z_B}\beta'+{1\over Z_C}\gamma' $$
纹理映射的问题
对于采样点 $(x,y)$ ，用重心坐标求出纹理坐标 $(u,v)$ ，将纹理值应用于采样点上。
纹理过小
$(u,v)$ 可能不是整数，用四舍五入等方式变成整数会导致纹理强行拉大（低分辨率强行拉成高分辨率），就会出现锯齿。
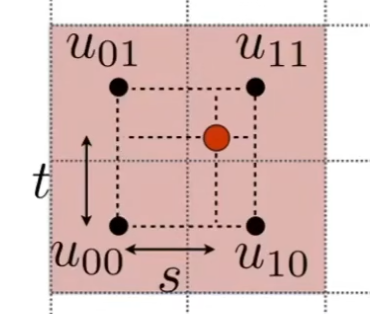
双线性插值：水平竖直均插值，$f(x,y)=lerp(t,lerp(s,u_{00},u_{10}),lerp(s,u_{01},u_{11}))$ 。
纹理过大
由于近大远小，远处的一个像素实际对应的3D表面/纹理区域很大，如果只采样这个像素点的纹理，就会走样（即采样频率过小）。
需要超采样，直接提高采样数量太费了。实际上超采样就是在求区域平均值，可以考虑预处理一下。
点查询 $\to$ 区域查询，使用 Mipmap 。
Mipmap
支持区域查询，但是是近似的，只能求正方形区域。
把纹理长宽不停缩短一半，得出 $\log$ 个新图（计算可得总大小多了 $1/3$ ），第 $D$ 层长宽缩短了 $2^D$ 倍。
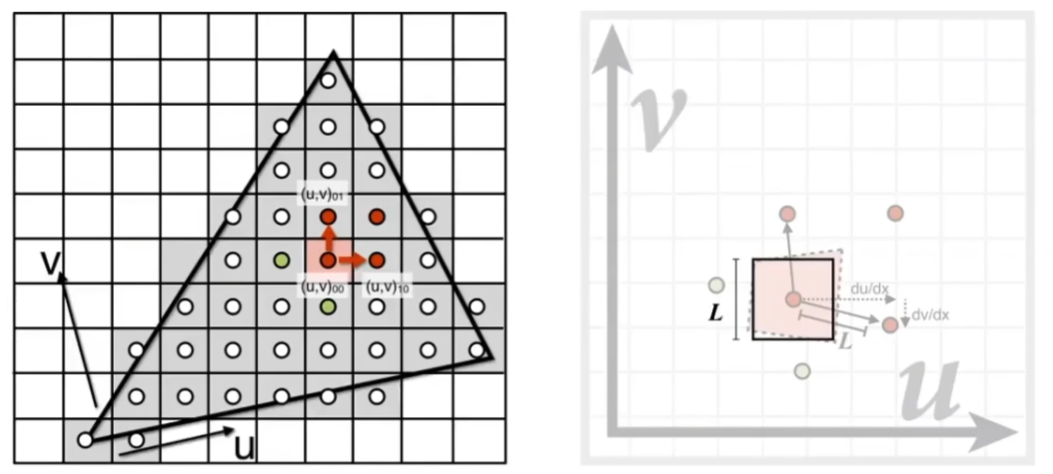
像素和相邻像素映射到纹理上，用纹理上的距离，求出近似的正方形区域长度 $L$ 。
$D=\log_2L$ ，在第 $D$ 层 Mipmap 上一个点就代表了 $L\times L$ 这个区域的值。
$D$ 不是整数？点也不是整数？没错又可以插值了，三线性插值：$D$ 层和 $D+1$ 层上双线性插值，然后再插值得到非整数层。
缺陷：实际上像素覆盖的纹理区域很可能不是正方形，导致 Mipmap 查询的区域大于实际区域，产生过分模糊。
Anisotropic Filtering 各向异性过滤
- Ripmap ：长宽独立缩短一半，得出 $\log\times\log$ 个新图（总大小多了 $3$ 倍），可以求矩形区域
- EWA 过滤：将不规则区域分为多个圆形多次查询
纹理的实际应用
环境映射：把环境光记录在纹理上
- Spherical Map 球面：记录在球面上，但展开成矩形后上下部分会扭曲
- Cube Map 立方体面：用立方体包围球，球面上的信息延半径往外延伸到立方体面上，展开六个面，可以减轻扭曲
凹凸贴图：改变表面的高度（高度变，引起的是法线等变了）
根据高度信息，利用梯度等计算新的法线。
本质上没有改变几何形状，边缘、阴影等方面无法表现。
位移贴图：改变表面的高度，但真的改变了顶点位置
需要模型比较精细，能够反映纹理的变化（即高采样频率）。
3D纹理：3D的噪声函数
不需要生成纹理图，将噪声经过处理后得出纹理
- 记录信息：例如记录颜色、阴影信息，用纹理的方式储存
6.几何
几何的表示
隐式：满足 $f(x,y,z)=0$ 的点
可能难以找出点形成的几何形体，但容易判定点是不是在形体上、形体内外等。
显式：用显式方法给出点集
- 参数映射（参数方程），例：$f(u,v)=(\cos u\sin v,\sin u\sin v,\cos v)$
- 点云：直接给点集
多边形面：把模型拆成多边形面（三角形、四边形）
The Wavefront Object File 格式 .obj ：文本文件，储存点坐标、法线、纹理坐标和它们的连接形式。
根据不同需求选择合适的表示方法。
隐式几何
- Constructive Solid Geometry，CSG ：通过几何求并、求交、求差等操作构造几何形体
- (Signed) Distance Function 距离函数：定义所有空间点到几何形体的最小距离（有正负，外部内部）
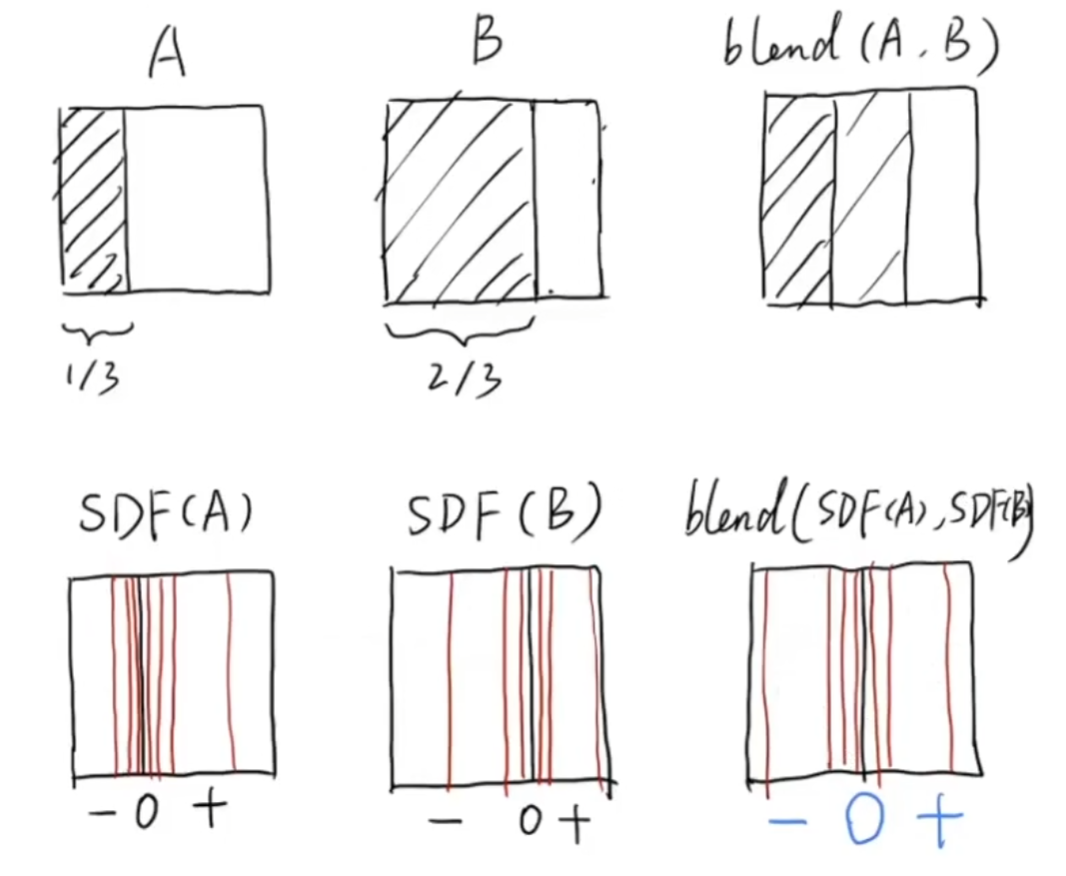
通过混合距离函数后还原的方式，可以混合几何形体的边界，实现平滑过渡。
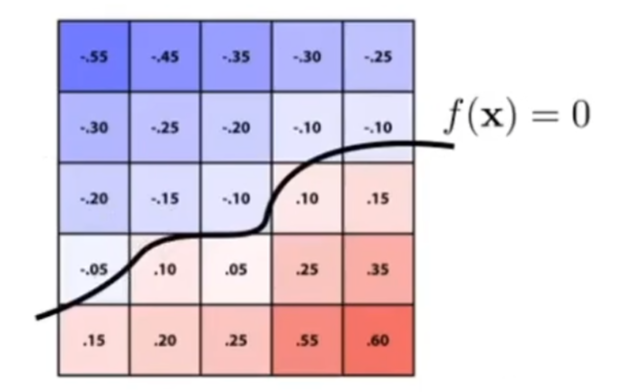
Level Set Methods 水平集：距离函数的一种表示方式，用网格表示函数值，插值为 $0$ 点的曲线就是边界
3D情况：可以找纹理的边界。
- 分形：自相似的几何形体（例如雪花）
显式几何 - 曲线
贝塞尔曲线：用一系列控制点定义曲线
控制点 $\{P_n\}=\{P_0,\cdots,P_n\}$ ，曲线经过 $P_0$ 和 $P_{n}$ ，不一定过中间点，用参数 $t(0\le t\le 1)$ 决定进度。
定义 $b_{1,i}(t)=lerp(t,P_i,P_{i+1}),b_{k,i}(t)=lerp(t,b_{k-1,i},b_{k-1,i+1})(k>1)$ 。
递推 $n$ 次后得到 $b_{n,0}(t)$ 表示 $t$ 进度时点的位置。
展开之后可以得到 $b_{n,0}(t)=\sum_{i=0}^{n}{n\choose i}t^i(1-t)^{n-i}P_i$（递推过程类似杨辉三角）。
贝塞尔曲线的性质
- $3$ 次贝塞尔曲线时，起点切线为 $3(P_1-P_0)$ ，终点切线为 $3(P_3-P_2)$
- $\{P_n\}$ 贝塞尔曲线仿射变换之后，和 $\{P_n\}$ 仿射变换之后的贝塞尔曲线相同
- 贝塞尔曲线一定在控制点形成的凸包内
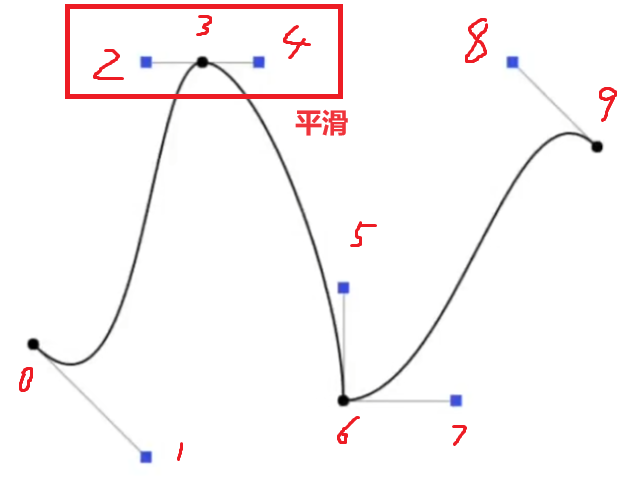
分段贝塞尔曲线：高次曲线不容易控制（中间可能会很平），可以每四个点构造 $3$ 次贝塞尔曲线
根据 $3$ 次贝塞尔曲线性质，只要上一段终点切线和下一段起点切线共线（控制点三点共线，一般还要等距），曲线就是平滑的
Spline 样条：经过一系列固定点的连续（可能是高阶连续）的曲线
B-spline (Basis spline) B样条：相比于贝塞尔曲线，调节控制点对曲线的影响具有局部性，比较复杂略过。
显式几何 - 曲面
贝塞尔曲面：用 $n\times m$ 控制点数组定义曲面
类似双线性插值：先构造 $m$ 个 $n-1$ 次贝塞尔曲线，$t_1$ 时刻的 $m$ 个曲线上的点再构造贝塞尔曲线 $t_2$ ，两个参数形成的点构成曲面。
表面网格操作 - 细分
Loop细分（不是循环细分，Loop是名字）：针对三角形网格细分，增加三角形、调整三角形位置
调整方法：增加三角形后产生新顶点，对于旧顶点和新顶点，用加权平均求出调整后的位置，使细分后的表面更光滑。
- Catmull-Clark细分：可以对四边形+三角形的混合网格进行细分
表面网格操作 - 简化
Edge Collapsing 边坍缩：删掉三角形一条边，把两个顶点合并
根据二次误差度量（衡量坍缩后和原轮廓的接近程度），每次贪心地选择误差最小的边来坍缩。
坍缩后边的误差会变化，因此需要用优先队列来维护。
- 表面网格操作 - 正则化：把三角形规范化，提升三角形质量，同时尽量不影响模型质量
7.光线追踪
Shadow Mapping 阴影贴图
核心思想：不是阴影的点，既能被光源（虚拟相机）看见，也能被相机看见。
相机看到的点，投影回光源的坐标系，通过深度缓存 z-buffer 即可判断该点是否被遮挡。
光源看向场景存下来的 z-buffer 深度图就是 Shadow Map 。也就是用光栅化来处理阴影。
问题：1. 只能处理硬阴影（点光源）。2. 存在大量的精度、走样问题（分辨率问题，类似纹理的走样）。
硬阴影和软阴影
硬阴影：点光源形成的阴影，一个点要么是阴影要么不是，边界分明。
软阴影：有大小的光源形成的阴影，阴影有过渡，从 umbra 本影过渡到 penumbra 半影过渡到没有阴影。
光线追踪和光栅化的对比
光线追踪优点：1. 可以处理软阴影。2. 可以处理光线多次反射。缺点：慢。
光栅化适合实时计算（快，质量较低），光线追踪适合离线计算（慢，质量高）。
光线追踪对光线的假设
- 光沿直线传播
- 光线不会相撞
- 光路可逆
和物理学有出入。
Ray Casting 光线投射
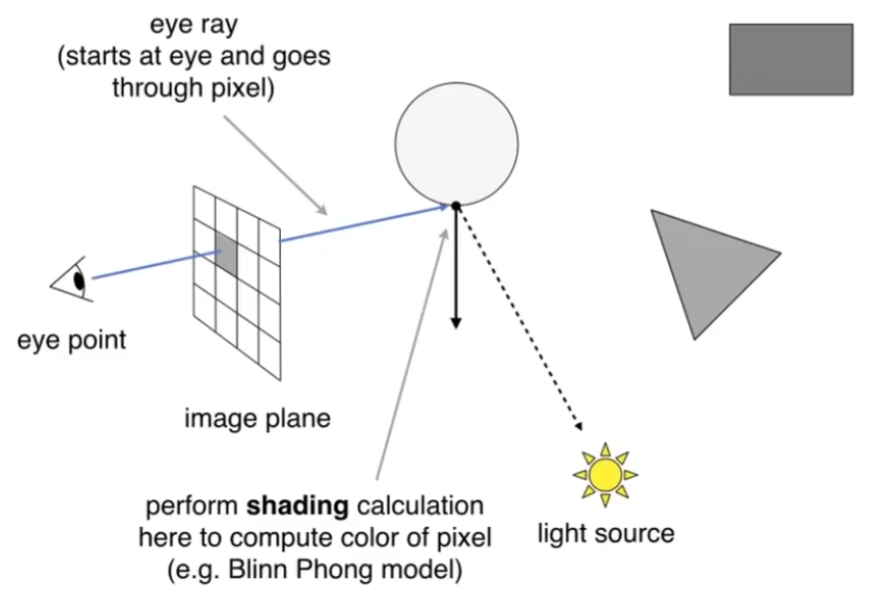
假设前提：眼睛是针孔相机（一个点）；光会发生完美的反射折射。
- 对每个像素，从相机投射一条光射线（eye ray）穿过这个像素，打到场景的模型上
- 打到场景的点后，再投射一条光射线（shadow ray）到光源，判断阴影、颜色等
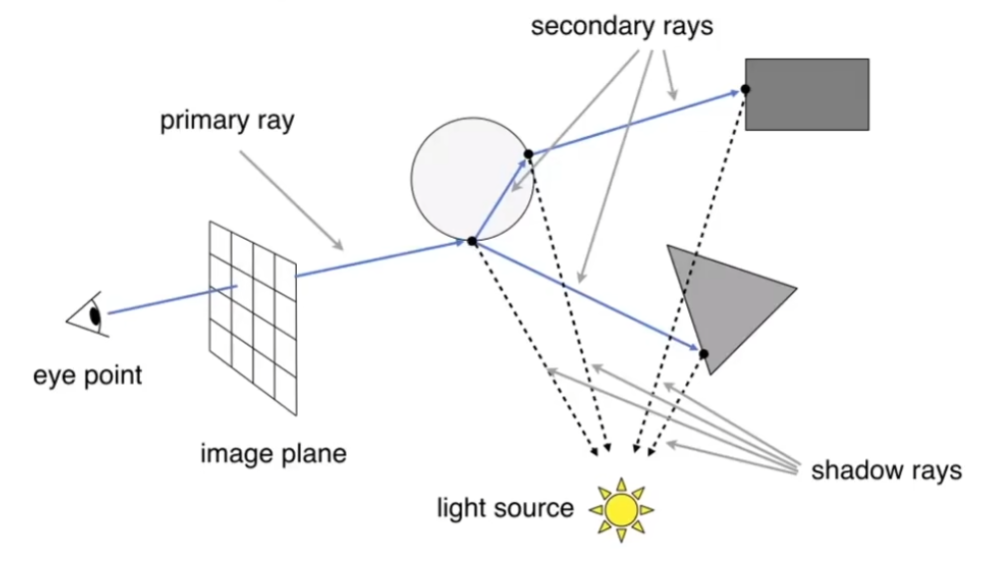
Whitted-style Ray Tracing 递归光线追踪
递归考虑光的反射和折射，把递归得到的 shadow rays 累加起来就可以得到像素的着色。
光线的计算
- 光线的定义：起点 $O$ 和方向 $\vec{d}$（单位向量），$\vec{r}(t)=O+t\vec{d},t\ge 0$
- 光与隐式表面 $f(P)=0$ 求交：求解 $f(O+t\vec{d})=0$ 即可
光与显式表面求交
最重要的是与三角形网格表面求交，即光与所有三角形求交。
只考虑 $0$ 个或 $1$ 个交点，不考虑光在三角形平面上。
- 光与三角形相交：简化为光与平面相交，然后判断交点是否在三角形内
光与三角形相交
平面的定义：平面上的点 $P'$ 和法线 $N$ ，平面方程为 $f(P)=(P-P')\cdot N=0$ 。
由 $(O+t\vec{d}-P')\cdot N=0$ 得 $t={(P'-O)\cdot N\over\vec{d}\cdot N}$ ，然后判定是否在三角形内。
更快的方法：Möller Trumbore 算法，用重心坐标求解参数，可以直接判定是否在三角形内。
Bounding Volumes 包围盒加速
暴力判断所有三角形太慢了！一个简单有效的优化：用一个盒子围住模型，如果光和包围盒都不相交，那么就不需要处理了。
AABB 包围盒（Axis-Aligned Bounding Box，轴对齐包围盒）：平行轴的长方体包围盒。
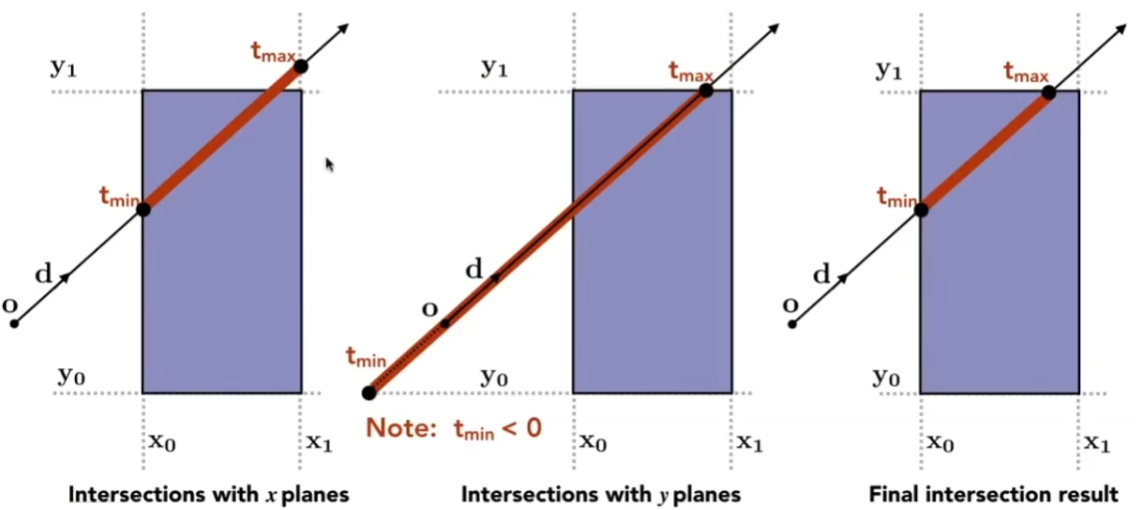
光和 AABB 相交（2D情况，3D同理）：
光线和 $x,y$ 边界分别求交，得到范围 $[tx_{min},tx_{max}],[ty_{min},ty_{max}]$ ，求交后得到光线与盒子的实际相交范围 $[t_{min},t_{max}]$ 。
3D情况：对 $x,y,z$ 面分别求交（由于轴对齐，比一般平面好求），三个时间范围求交后得到 $[t_{enter},t_{exit}]$ 。
$t_{enter}<t_{exit},t_{exit}\ge 0$ 时，光线经过了 AABB 。
空间划分 - KDTree
把包围盒划分为许多小的盒子，与包围盒求交继续细分为和小盒子求交。
均匀划分：把包围盒划分为规则的网格
实际场景中物体分布并不均匀，因此这个方法效率不高。
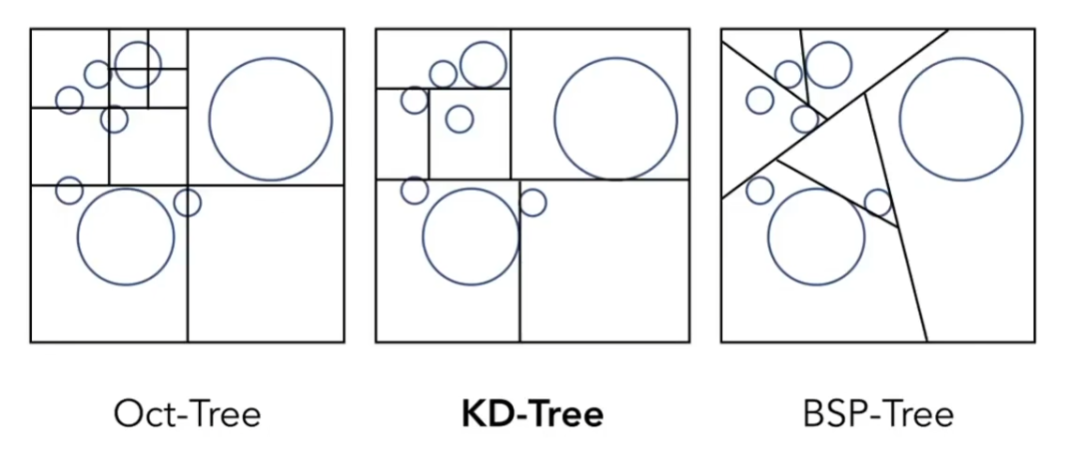
非均匀划分：使用 Oct-Tree 、KD-Tree 、BSP-Tree 等数据结构划分
划分到子空间含有较少物体为止。
KD-Tree 划分：对每个维度（ $x\to y\to z\to x\to\cdots$ ）交替划分，形成二叉树结构。
节点信息：
- 该节点的空间范围（AABB 情况下，子空间也是 AAB）
- 两个儿子
- 只在叶子节点上储存物体列表
查询时递归查询光线是否和子空间相交，遇到叶子节点后和物体求交。
KD-Tree 的问题：
- 判断物体和子空间是否相交很困难
- 一个物体可能会在很多叶子节点中
物体划分 - BVH
反过来考虑，不对空间划分，对物体划分。
BVH (Bounding Volume Hierarchy)：每次将物体分为两部分，形成二叉树结构，节点储存包围盒，只在叶子节点储存物体列表。
和 KD-Tree 的对比：
- 一个物体只会出现在一个叶子节点上
- 包围盒容易求
- 空间有重叠（因此划分方式很有讲究）
一些划分方式：
- 按照最长的轴划分（减少重叠）
- 按照中间物体划分（左右物体数尽可能均匀）
查询类似 KDT 。
8.辐射度量学
Radiometry 辐射度量学
为什么要辐射度量学&路径追踪：
- Blinn-Phong 模型中含有大量简化，例如光强没有单位只是个数字，不能精确描述光的传播
Whitted 风格光线追踪的问题：只在镜面反射面上反射和折射，漫反射面不处理
Color bleeding ：一种全局光照的效果，有颜色的漫反射面会把颜色渗透到其他面上（Whitted 风格光线追踪无法处理）。
辐射度量学：在物理上精准描述光照的方法。
物理量
Radiant Energy and Flux
- Radiant energy ：光的能量 $Q$ ，单位焦耳 $J$
Radiant flux ：光的功率 $\Phi$ ，单位瓦特 $W$ / 流明 $lm$（光学单位）
光学意义：代表单位时间通过的光子数量（光通量）
Radiant Intensity ：每单位立体角光的功率 $I(\omega)={d\Phi\over d\omega}$ ，单位坎德拉 $cd$
立体角：角在三维空间的延申，在球上，从圆心射出一个锥，打到球面上得到面积 $A$ ，定义该立体角为 $\Omega={A\over r^2}$ 。
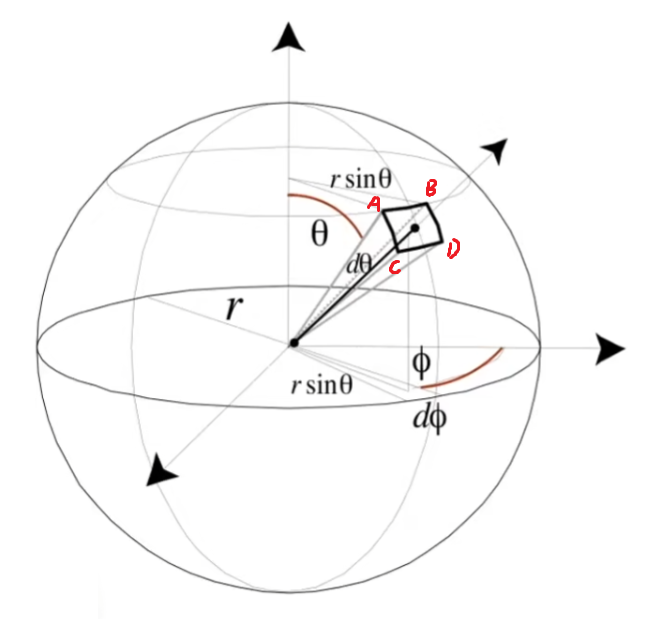
单位立体角（微分立体角）：从点 $(r\sin\theta\cos\phi,r\sin\theta\sin\phi,r\cos\theta)$ 往外 $d\theta,d\phi$ 形成的面的立体角。可以用向量 $d\omega$ 来代表。
$$ dA=AB\cdot AC=r\sin\theta\,d\phi\cdot r\,d\theta=r^2\sin\theta\,d\phi\,d\theta\\ d\omega={dA\over r^2}=\sin\theta\,d\phi\,d\theta\\ \text{Sphere: }\Omega=\int_{S^2}d\omega=\int_{0}^{2\pi}\left(\int_{0}^{\pi}\sin\theta\,d\theta\right)d\phi=\int_{0}^{2\pi}2\,d\phi=4\pi $$
Radiant Irradiance ：每单位面积接收到的垂直的光的功率 $E(x)={d\Phi(x)\over dA}$ ，单位 $lux$
Blinn-Phong 模型中需要考虑入射夹角、以及能量衰减除以 $r^2$ 都能用 irradiance 解释。
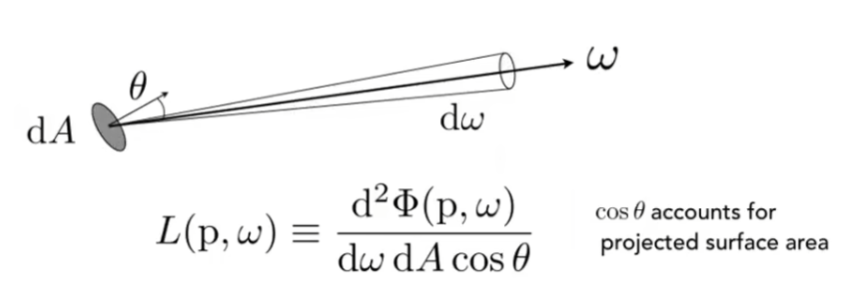
Radiance ：用于描述光线的属性，光在单位投影面积、单位立体角的功率 $L(p,\omega)={d^2\Phi(p,\omega)\over d\omega\,dA\cos\theta}$ ，单位 $nit$
既可以是 irradiance 在单位立体角上的值，也可以是 intensity 在单位投影面积上的值。
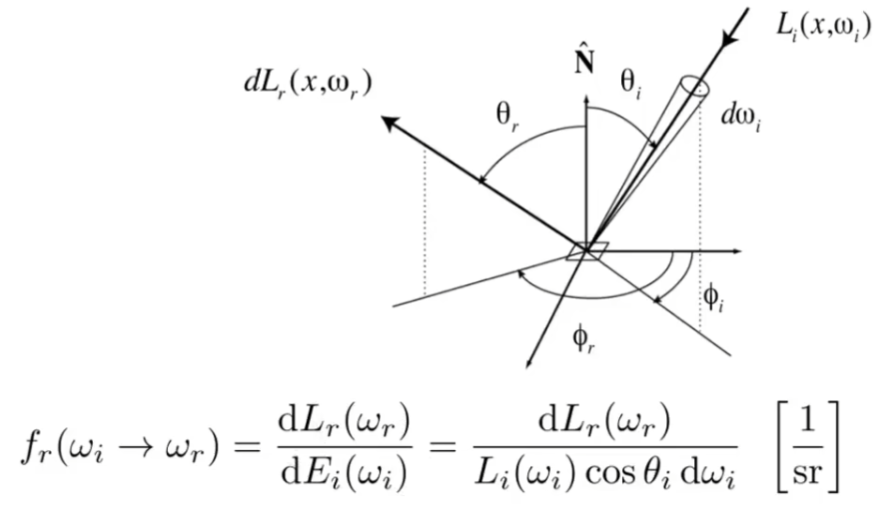
BRDF 双向反射分布函数
描述反射：一个表面 $dA$ 上，从某个方向进入的 radiance 被表面吸收为 irradiance ，然后朝不同方向反射 radiance 。
Bidirectional Reflectance Distribution Function (BRDF) ：定义 irradiance 如何分配到各个方向。
反射方程
已知 BRDF 后，通过累加每个方向的 radiance 和 BRDF ，就可以得到任一方向的反射 radiance 。
问题：这个方程是递归的，反射光经过其他反射之后会变成入射光。
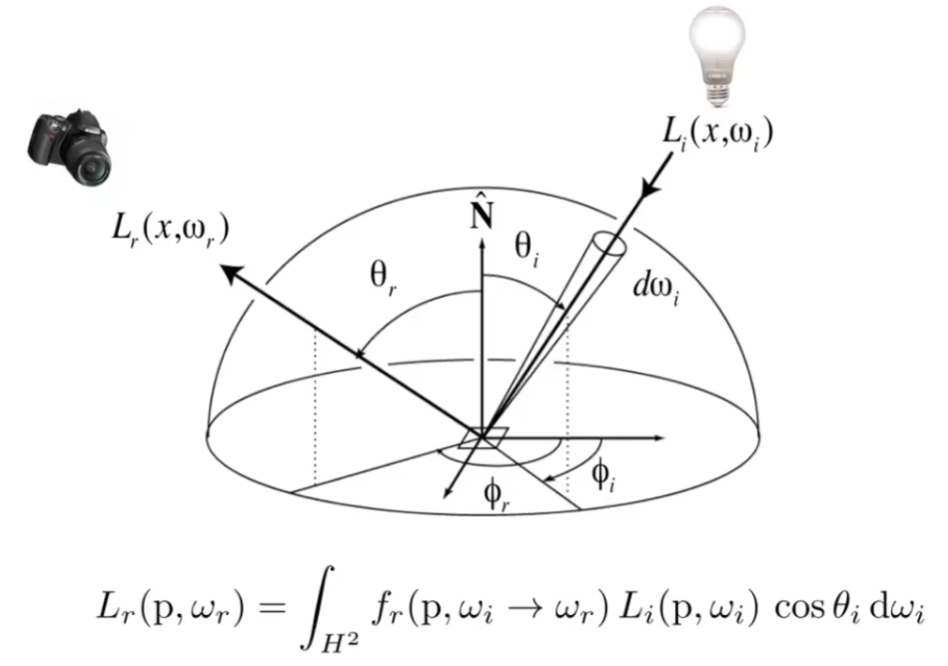
渲染方程
物体的反射项加上自身的发光项，得到渲染方程：
$$ L_o(p,\omega_o)=L_e(p,\omega_o)+\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(\vec{n}\cdot\vec{\omega}_i)\,d\omega_i $$
$\Omega^+$ 表示上半球面（夹角超过直角的部分没有反射意义），$\vec{\omega}_i$ 方向朝外，$\vec{n}\cdot\vec{\omega}_i$ 即 $\cos\theta_i$ 。
该方程可以统一所有光线传播，例如点光源、面光源（点光源的积分）、多次反射（反射面也当成光源）等。
渲染方程是物理上精确的。
蒙特卡洛积分
一种数值方法，用于解决解析式不好处理的定积分 $\int_{a}^{b}f(x)\,dx$ 。
在定积分域上随机采样 $X_i\sim p(x)$ ，则定积分可以近似成 $F_N={1\over N}\sum_{i=1}^{N}{f(X_i)\over p(X_i)}$ 。
均匀采样时：$F_N={1\over N}\sum_{i=1}^{N}{f(X_i)\over p(X_i)}={1\over N}\sum_{i=1}^{N}{f(X_i)\over 1/(b-a)}={b-a\over N}\sum_{i=1}^{N}f(X_i)$ 。
$N$ 越大，误差越小。
渲染方程的计算
方程虽然是递归的，但是除了反射项之外都是已知的，我们可以通过转化，把方程变为一种算子形式：
$$ L=E+KL\\ L=(1-K)^{-1}E=(1+K+K^2+\cdots)E=E+KE+K^2E+\cdots $$
可以发现 $E$ 是光源项，$KE$ 是直接光照（弹射一次），$K^tE,t>1$ 是弹射 $t$ 次后的间接光照。$K^tE,t\ge 1$ 的和为全局光照（直接+间接光照）。
普通的光栅化只能处理光源+直接光照，需要光线追踪处理间接光照。
渲染方程的积分即半球面上的定积分，可以用蒙特卡洛积分来近似。
只考虑直接光照时，对 $\omega_i\sim pdf(\omega)$ 随机采样：
$$ \begin{aligned} L_o(p,\omega_o)&=\int_{\Omega^+}L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(\vec{n}\cdot\vec{\omega}_i)\,d\omega_i\\ &\approx{1\over N}\sum_{i=1}^{N}{L_i(p,\omega_i)f_r(p,\omega_i,\omega_o)(\vec{n}\cdot\vec{\omega}_i)\over pdf(\omega_i)}\\ &={1\over N}\sum_{i=1}^{N}L_i(p,\omega_i)\cdot val(p,\omega_i,\omega_o) \end{aligned} $$
把这个过程定义为 $shade(p,\omega_o)$ ：
- 随机采样 $N$ 个 $\omega_i$
- 从 $p$ 打出光线 $\omega_i$ ，如果打到了光源 $L_i$ ，则 $L_o$ 累加 $L_i\cdot val(p,\omega_i,\omega_o)$
- 结果为 $L_o$
扩展到全局光照（直接+间接），只需要递归定义一下：
- 随机采样 $N$ 个 $\omega_i$
从 $p$ 打出光线 $\omega_i$
- 如果打到了光源 $L_i$ ，则 $L_o$ 累加 $L_i\cdot val(p,\omega_i,\omega_o)$
- 如果打到了物体 $q$ ，则 $L_o$ 累加 $shade(q,-\omega_i)\cdot val(p,\omega_i,\omega_o)$
- 结果为 $L_o$
问题1：递归下去，光线的数量指数爆炸了。
问题2：这个递归是没有边界的。
Path Tracing 路径追踪
路径追踪是对渲染方程计算的解决方式：
解决问题1：用 $N=1$ 处理 $shade(p,\omega_o)$ ，不会出现指数爆炸
只用一根光线效果太差了，但是像素着色时我们可以多采样几次求平均 $shade$ 来解决。
如何求一个像素的 radiance（也是个蒙特卡洛积分）：
- 随机采样 $N$ 个像素上的位置
- 从相机到采样点打出一条光线 $\omega_i$ ，在场景中打到 $p$ ，累加 $shade(p,-\omega_i)$
- 求平均得到结果
解决问题2：Russian Roulette (RR) 俄罗斯轮盘赌
每次有 $P(0<P<1)$ 的概率打光线得到结果 $L_o\over P$ ，$1-P$ 的概率不打光线直接返回 $0$ 。
期望结果为 $E=P\cdot {L_o\over P}+(1-P)\cdot 0=L_o$ ，也就是说期望结果是对的。
路径追踪的优化：
对采样的优化：如果以均匀概率对单位立体角采样，低采样次数下效果不好（即采样效率低下），原因是很多光线打空了
如果概率集中在光源上，就可以提高采样效率。
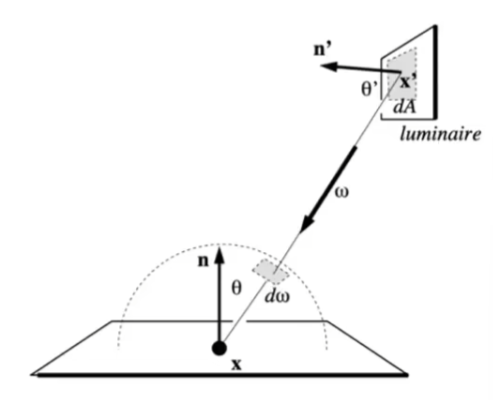
直接考虑在光源面 $dA$ 上采样！需要把 $d\omega$ 转化为 $dA$ ，改写积分式，在 $dA$ 的积分上做蒙特卡洛积分。
把 $dA$ 转到和 $d\omega$ 垂直，然后缩放 $x$ 点到 $x'$ 点的距离倍，就可以转化为单位立体角。
$$ d\omega={dA\cos\theta'\over\Vert x-x'\Vert^2}\\ \begin{aligned} L_o(x,\omega_o)&=\int_{\Omega^+}L_i(x,\omega_i)f_r(x,\omega_i,\omega_o)\cos\theta_i\,d\omega_i\\ &=\int_{A}L_i(x,\omega_i)f_r(x,\omega_i,\omega_o){\cos\theta_i\cos\theta'_i\over\Vert x-x'_i\Vert^2}\,dA_i\\ \end{aligned} $$
注意：$x\to x'$ 路径上如果打到物体，则结果是 $0$ 。
然后把 $shade$ 拆成两部分：直接光照（使用 $dA$ 采样，不需要 RR ），间接光照（使用 $d\omega$ 采样，需要 RR ）。
- 点光源无法处理：建议把点光源做成很小面积的面光源
Homework
Homework1 - 观测变换
// 模型变换矩阵，绕 Z 轴旋转
Eigen::Matrix4f get_model_matrix(float rotation_angle)
{
Eigen::Matrix4f model = Eigen::Matrix4f::Identity();
float theta = rotation_angle / 180 * MY_PI;
model << cos(theta), -sin(theta), 0, 0,
sin(theta), cos(theta), 0, 0,
0, 0, 1, 0,
0, 0, 0, 1;
return model;
}
// 投影矩阵
Eigen::Matrix4f get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
{
float n = -zNear, f = -zFar;
float fov = eye_fov / 180 * MY_PI;
float t = tan(fov / 2) * fabs(n);
float r = t * aspect_ratio;
// 透视投影矩阵
Eigen::Matrix4f Pe = Eigen::Matrix4f::Identity();
Pe << n, 0, 0, 0,
0, n, 0, 0,
0, 0, n + f, -n * f,
0, 0, 1, 0;
// 正交投影矩阵 [-r,r]*[-t,t]*[n,f]
Eigen::Matrix4f Or = Eigen::Matrix4f::Identity();
Or << 1 / r, 0, 0, 0,
0, 1 / t, 0, 0,
0, 0, 2 / (f - n), -(n + f) / 2,
0, 0, 0, 1;
return Or * Pe;
}Homework2 - 光栅化
超采样需要对每个像素中细分出来的点储存深度值和颜色值，否则会出现黑边。
如果颜色只存在像素上，三角形相交区域的边界上只会储存最上面三角形的颜色，无法与其他三角形混合，因此颜色会没有过渡出现黑边。
rasterizer.cpp的部分代码如下：
static bool insideTriangle(float x, float y, const Vector3f* _v)
{
Vector2f P(x, y);
Vector2f v[3] = {
Vector2f(_v[0].x(), _v[0].y()),
Vector2f(_v[1].x(), _v[1].y()),
Vector2f(_v[2].x(), _v[2].y())};
int sign = 0;
auto Cross = [](const Vector2f &a, const Vector2f &b) { return a.x() * b.y() - a.y() * b.x(); };
for (int i = 0; i < 3; i++)
{
// 求二维叉乘值
float val = Cross(v[(i + 1) % 3] - v[i], P - v[i]);
// 在三角形边上
if (fabs(val) < 1e-8)
return true;
if (!sign)
sign = (val < 0 ? -1 : 1);
// 叉乘正负性不相同，不在三角形内部
if ((val < 0 ? -1 : 1) != sign)
return false;
}
return true;
}
// Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle &t)
{
auto v = t.toVector4();
// 求出 bounding box
float L = std::min({v[0].x(), v[1].x(), v[2].x()});
float R = std::max({v[0].x(), v[1].x(), v[2].x()});
float B = std::min({v[0].y(), v[1].y(), v[2].y()});
float T = std::max({v[0].y(), v[1].y(), v[2].y()});
for (int px = L; px <= R; px++)
for (int py = B; py <= T; py++)
{
// 2x2 的超采样
int count = 0;
for (int i = 0; i < 2; i++)
for (int j = 0; j < 2; j++)
{
float x = px + (i + 0.5) / 2, y = py + (j + 0.5) / 2;
if (insideTriangle(x, y, t.v))
{
count++;
// 用重心坐标进行深度插值
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float w_reciprocal = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
float z_interpolated = alpha * v[0].z() / v[0].w() + beta * v[1].z() / v[1].w() + gamma * v[2].z() / v[2].w();
z_interpolated *= w_reciprocal;
// z-buffer
int index = get_index(px, py) + (i << 1) + j;
if (z_interpolated < depth_buf[index])
{
depth_buf[index] = z_interpolated;
color_buf[index] = t.getColor();
}
}
}
if (count > 0)
{
int index = get_index(px, py);
Vector3f color = (color_buf[index] + color_buf[index + 1] + color_buf[index + 2] + color_buf[index + 3]) / 4;
set_pixel(Vector3f(px, py, 0), color);
}
}
}
void rst::rasterizer::clear(rst::Buffers buff)
{
if ((buff & rst::Buffers::Color) == rst::Buffers::Color)
{
std::fill(frame_buf.begin(), frame_buf.end(), Eigen::Vector3f{0, 0, 0});
std::fill(color_buf.begin(), color_buf.end(), Eigen::Vector3f{0, 0, 0});
}
if ((buff & rst::Buffers::Depth) == rst::Buffers::Depth)
{
std::fill(depth_buf.begin(), depth_buf.end(), std::numeric_limits<float>::infinity());
}
}
rst::rasterizer::rasterizer(int w, int h) : width(w), height(h)
{
frame_buf.resize(w * h);
depth_buf.resize(w * h * 4);
color_buf.resize(w * h * 4);
}
int rst::rasterizer::get_index(int x, int y)
{
return ((height - 1 - y) * width + x) * 4;
}Homework3 - 着色&纹理映射
rasterizer.cpp的部分代码：
// Screen space rasterization
void rst::rasterizer::rasterize_triangle(const Triangle &t, const std::array<Eigen::Vector3f, 3> &view_pos)
{
auto v = t.toVector4();
// 求出 bounding box
float L = std::min({v[0].x(), v[1].x(), v[2].x()});
float R = std::max({v[0].x(), v[1].x(), v[2].x()});
float B = std::min({v[0].y(), v[1].y(), v[2].y()});
float T = std::max({v[0].y(), v[1].y(), v[2].y()});
for (int px = L; px <= R; px++)
for (int py = B; py <= T; py++)
{
float x = px + 0.5, y = py + 0.5;
if (insideTriangle(x, y, t.v))
{
// 用重心坐标进行深度插值，需要进行透视投影矫正
auto [alpha, beta, gamma] = computeBarycentric2D(x, y, t.v);
float Z = 1.0 / (alpha / v[0].w() + beta / v[1].w() + gamma / v[2].w());
alpha *= Z / v[0].w();
beta *= Z / v[1].w();
gamma *= Z / v[2].w();
float zp = alpha * v[0].z() + beta * v[1].z() + gamma * v[2].z();
// z-buffer
int index = get_index(px, py);
if (zp < depth_buf[index])
{
depth_buf[index] = zp;
// 插值信息
Vector3f color = alpha * t.color[0] + beta * t.color[1] + gamma * t.color[2];
Vector3f normal = alpha * t.normal[0] + beta * t.normal[1] + gamma * t.normal[2];
Vector2f texcoords = alpha * t.tex_coords[0] + beta * t.tex_coords[1] + gamma * t.tex_coords[2];
Vector3f shadingcoords = alpha * view_pos[0] + beta * view_pos[1] + gamma * view_pos[2];
// 着色
fragment_shader_payload payload(color, normal.normalized(), texcoords, texture ? &*texture : nullptr);
payload.view_pos = shadingcoords;
auto pixel_color = fragment_shader(payload);
set_pixel(Vector2i(px, py), pixel_color);
}
}
}
}main.cpp的部分代码：
Eigen::Vector3f texture_fragment_shader(const fragment_shader_payload &payload)
{
Eigen::Vector3f return_color = {0, 0, 0};
if (payload.texture)
{
return_color = payload.texture->getColor(payload.tex_coords[0], payload.tex_coords[1]);
}
Eigen::Vector3f texture_color;
texture_color << return_color.x(), return_color.y(), return_color.z();
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = texture_color / 255.f;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = texture_color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
Vector3f v = (eye_pos - point).normalized(); // 观察方向
auto Scale = [](const Vector3f &s, const Vector3f &a) { return Vector3f(s.x() * a.x(), s.y() * a.y(), s.z() * a.z()); };
for (auto &light : lights)
{
Vector3f l = light.position - point; // 光照方向
float r2 = l.squaredNorm(); // 距离平方
l.normalize();
Vector3f diffuse = Scale(kd, light.intensity / r2) * std::max(0.0f, l.dot(normal)); // 漫反射项
Vector3f h = (v + l).normalized(); // 半程向量
Vector3f specular = Scale(ks, light.intensity / r2) * std::pow(std::max(0.0f, h.dot(normal)), p); // 镜面反射项
Vector3f ambient = Scale(ka, amb_light_intensity); // 间接光照项
result_color += diffuse + specular + ambient;
}
return result_color * 255.f;
}
Eigen::Vector3f phong_fragment_shader(const fragment_shader_payload &payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
Eigen::Vector3f result_color = {0, 0, 0};
Vector3f v = (eye_pos - point).normalized(); // 观察方向
auto Scale = [](const Vector3f &s, const Vector3f &a) { return Vector3f(s.x() * a.x(), s.y() * a.y(), s.z() * a.z()); };
for (auto &light : lights)
{
Vector3f l = light.position - point; // 光照方向
float r2 = l.squaredNorm(); // 距离平方
l.normalize();
Vector3f diffuse = Scale(kd, light.intensity / r2) * std::max(0.0f, l.dot(normal)); // 漫反射项
Vector3f h = (v + l).normalized(); // 半程向量
Vector3f specular = Scale(ks, light.intensity / r2) * std::pow(std::max(0.0f, h.dot(normal)), p); // 镜面反射项
Vector3f ambient = Scale(ka, amb_light_intensity); // 间接光照项
result_color += diffuse + specular + ambient;
}
return result_color * 255.f;
}
Eigen::Vector3f displacement_fragment_shader(const fragment_shader_payload &payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement displacement mapping here
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
// Vector b = n cross product t
// Matrix TBN = [t b n]
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
// Vector ln = (-dU, -dV, 1)
// Position p = p + kn * n * h(u,v)
// Normal n = normalize(TBN * ln)
Vector3f n = normal;
float nx = n.x(), ny = n.y(), nz = n.z();
Vector3f t(nx * ny / sqrt(nx * nx + nz * nz), sqrt(nx * nx + nz * nz), nz * ny / sqrt(nx * nx + nz * nz));
Vector3f b = n.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), n.x(),
t.y(), b.y(), n.y(),
t.z(), b.z(), n.z();
float w = payload.texture->width, h = payload.texture->height; // 纹理长宽
float u = payload.tex_coords[0], v = payload.tex_coords[1]; // 纹理坐标
float dU = kh * kn * (payload.texture->getColor(u + 1 / w, v).norm() - payload.texture->getColor(u, v).norm()); // 梯度
float dV = kh * kn * (payload.texture->getColor(u, v + 1 / h).norm() - payload.texture->getColor(u, v).norm());
Vector3f ln(-dU, -dV, 1);
point += kn * n * payload.texture->getColor(u, v).norm(); // 位移后的位置
normal = (TBN * ln).normalized(); // 新的法线
Eigen::Vector3f result_color = {0, 0, 0};
Vector3f V = (eye_pos - point).normalized(); // 观察方向
auto Scale = [](const Vector3f &s, const Vector3f &a) { return Vector3f(s.x() * a.x(), s.y() * a.y(), s.z() * a.z()); };
for (auto &light : lights)
{
Vector3f l = light.position - point; // 光照方向
float r2 = l.squaredNorm(); // 距离平方
l.normalize();
Vector3f diffuse = Scale(kd, light.intensity / r2) * std::max(0.0f, l.dot(normal)); // 漫反射项
Vector3f h = (V + l).normalized(); // 半程向量
Vector3f specular = Scale(ks, light.intensity / r2) * std::pow(std::max(0.0f, h.dot(normal)), p); // 镜面反射项
Vector3f ambient = Scale(ka, amb_light_intensity); // 间接光照项
result_color += diffuse + specular + ambient;
}
return result_color * 255.f;
}
Eigen::Vector3f bump_fragment_shader(const fragment_shader_payload &payload)
{
Eigen::Vector3f ka = Eigen::Vector3f(0.005, 0.005, 0.005);
Eigen::Vector3f kd = payload.color;
Eigen::Vector3f ks = Eigen::Vector3f(0.7937, 0.7937, 0.7937);
auto l1 = light{{20, 20, 20}, {500, 500, 500}};
auto l2 = light{{-20, 20, 0}, {500, 500, 500}};
std::vector<light> lights = {l1, l2};
Eigen::Vector3f amb_light_intensity{10, 10, 10};
Eigen::Vector3f eye_pos{0, 0, 10};
float p = 150;
Eigen::Vector3f color = payload.color;
Eigen::Vector3f point = payload.view_pos;
Eigen::Vector3f normal = payload.normal;
float kh = 0.2, kn = 0.1;
// TODO: Implement bump mapping here
// Let n = normal = (x, y, z)
// Vector t = (x*y/sqrt(x*x+z*z),sqrt(x*x+z*z),z*y/sqrt(x*x+z*z))
// Vector b = n cross product t
// Matrix TBN = [t b n]
// dU = kh * kn * (h(u+1/w,v)-h(u,v))
// dV = kh * kn * (h(u,v+1/h)-h(u,v))
// Vector ln = (-dU, -dV, 1)
// Normal n = normalize(TBN * ln)
Vector3f n = normal;
float nx = n.x(), ny = n.y(), nz = n.z();
Vector3f t(nx * ny / sqrt(nx * nx + nz * nz), sqrt(nx * nx + nz * nz), nz * ny / sqrt(nx * nx + nz * nz));
Vector3f b = n.cross(t);
Matrix3f TBN;
TBN << t.x(), b.x(), n.x(),
t.y(), b.y(), n.y(),
t.z(), b.z(), n.z();
float w = payload.texture->width, h = payload.texture->height; // 纹理长宽
float u = payload.tex_coords[0], v = payload.tex_coords[1]; // 纹理坐标
float dU = kh * kn * (payload.texture->getColor(u + 1 / w, v).norm() - payload.texture->getColor(u, v).norm()); // 梯度
float dV = kh * kn * (payload.texture->getColor(u, v + 1 / h).norm() - payload.texture->getColor(u, v).norm());
Vector3f ln(-dU, -dV, 1);
normal = (TBN * ln).normalized(); // 新的法线
Eigen::Vector3f result_color = {0, 0, 0};
result_color = normal;
return result_color * 255.f;
}
zzk狠狠学cg然后去乱杀
