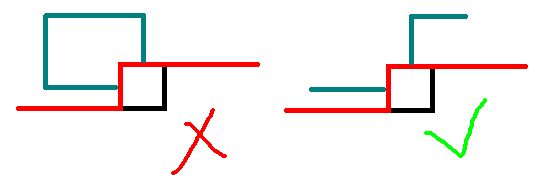题目概述

给出 $n\times m$ 的网格图，其中有些格子是障碍，求有多少种方法用一条哈密顿回路覆盖没有障碍的格子。

解题报告

ps：大量图片来自于cdq的课件QAQ。

这道题的退化版是HDU1693。由于只能用一条哈密顿回路，所以在两个位置都有插头的时候不一定能直接接起来，因为如果这两个插头是连通的，在当前格子接起来就会形成回路，导致出现多条哈密顿回路（除非已经处理到了最后一个非障碍格子）。

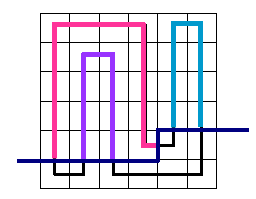
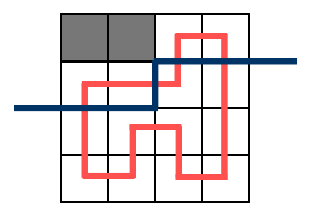
也就是说只记录轮廓线上是否有插头是不够的，我们还需要知道插头连出去的情况。观察轮廓线会把哈密顿回路切成什么样：

会发现切成了若干条路径，并且路径不可能相交，这就使我们想到了括号序列！

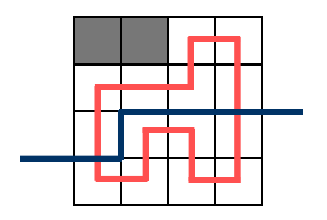
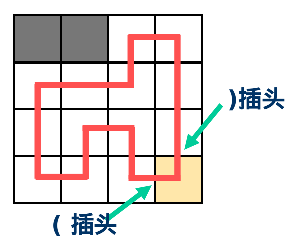
于是就有一个三进制的状压DP，$0$ 表示没有插头，$1$ 表示有左括号插头，$2$ 表示有右括号插头。

接下来就是大力分类讨论（用 $A,B$ 表示当前两个位置的状态）：

1. $A=0,B=0​$ ：

   

   当前格子一定有右插头和下插头。

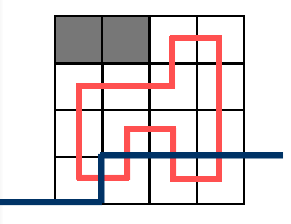
2. $A=1,B=1$ 或 $A=2,B=2$ ：

   

   当前格子一定有左插头和上插头，由于合并了两条路径，所以需要找到 $B$ 匹配的右括号插头（ $A​$ 匹配的左括号），将其改为左括号插头（右括号插头），可以预处理。

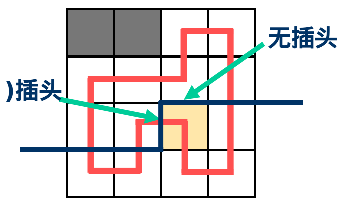
3. $A=2,B=1$ ：

   

   当前格子一定有左插头和上插头，相当于合并了两条路径。

4. $A=1,B=2$ ：

   

   只有在最后一个非障碍格子中才可以进行转移，相当于形成了哈密顿回路。

5. $A,B$ 中有一个是 $0$ ：

   

   一定有左插头或上插头，右插头和下插头可以选一个，相当于延长了原来的路径。

为了写起来方便我们可以用四进制而不是三进制，因为空间限制很紧，需要用哈希表进行时空优化（很多状态是没用的）。

示例程序

#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long LL;
const int maxn=12,maxm=12,maxs=1594323,HA=23333;

int n,m,X,Y;char pic[maxn+5][maxm+5];
struct Hashmap{
    int lnk[HA],E,nxt[maxs+5],son[maxs+5];LL w[maxs+5];
    inline void Clear() {for (int i=0;i<HA;i++) lnk[i]=0;E=0;}
    inline void Add(int x,int y) {son[++E]=y;w[E]=0;nxt[E]=lnk[x];lnk[x]=E;}
    inline LL& operator [] (const int &x){
        for (int j=lnk[x%HA];j;j=nxt[j]) if (son[j]==x) return w[j];
        Add(x%HA,x);return w[E];
    }
}f[2];

#define val(s,i) ((s)>>(i<<1)&3)
#define LB(i) (1<<(i<<1))
#define RB(i) (2<<(i<<1))
int main(){
    freopen("program.in","r",stdin);freopen("program.out","w",stdout);
    scanf("%d%d",&n,&m);for (int i=1;i<=n;i++) scanf("%s",pic[i]+1);f[0][0]=1;
    for (X=n;X;X--) {for (Y=m;Y&&pic[X][Y]!='.';Y--);if (pic[X][Y]) break;}
    for (int i=1,c=1;i<=X;i++){
        LL F;f[c].Clear();for (int e=1;e<=f[c^1].E;e++) if (F=f[c^1].w[e]) f[c][f[c^1].son[e]<<2]+=F;
        for (int j=(f[c^1]=f[c],1);i<X?j<=m:j<=Y;j++,c^=1)
            for (int e=(f[c].Clear(),1);e<=f[c^1].E;e++){
                int s=f[c^1].son[e];LL F=f[c^1].w[e];if (!F) continue;int A=val(s,j-1),B=val(s,j);
                if (pic[i][j]=='*') {if (!A&&!B) f[c][s]+=F;}
                else if (A==1&&!B){
                    if (pic[i][j+1]=='.') f[c][s^LB(j-1)^LB(j)]+=F;
                    if (pic[i+1][j]=='.') f[c][s]+=F;
                } else if (A==2&&!B){
                    if (pic[i][j+1]=='.') f[c][s^RB(j-1)^RB(j)]+=F;
                    if (pic[i+1][j]=='.') f[c][s]+=F;
                } else if (!A&&B==1){
                    if (pic[i][j+1]=='.') f[c][s]+=F;
                    if (pic[i+1][j]=='.') f[c][s^LB(j)^LB(j-1)]+=F;
                } else if (!A&&B==2){
                    if (pic[i][j+1]=='.') f[c][s]+=F;
                    if (pic[i+1][j]=='.') f[c][s^RB(j)^RB(j-1)]+=F;
                } else if (A==1&&B==1){
                    int k,num=1;for (k=j+1;num;k++) val(s,k)==2?num--:num+=val(s,k);
                    k--;f[c][s^LB(j-1)^LB(j)^RB(k)^LB(k)]+=F;
                } else if (A==2&&B==2){
                    int k,num=-1;for (k=j-2;num;k--) val(s,k)==2?num--:num+=val(s,k);
                    k++;f[c][s^RB(j-1)^RB(j)^LB(k)^RB(k)]+=F;
                } else if (A==2&&B==1) f[c][s^RB(j-1)^LB(j)]+=F;
                else if (A==1&&B==2) {if (i==X&&j==Y) f[c][s^LB(j-1)^RB(j)]+=F;}
                else if (pic[i][j+1]=='.'&&pic[i+1][j]=='.') f[c][s^LB(j-1)^RB(j)]+=F;
            }
    }printf("%lld\n",f[(X-1)*m+Y&1][0]);return 0;
}