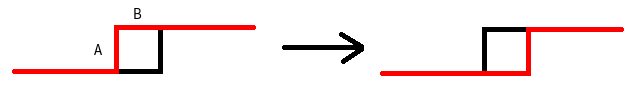题目概述

给出 $n\times m$ 的网格图，其中有些格子是障碍，求有多少种方法用若干个哈密顿回路覆盖没有障碍的格子。

解题报告

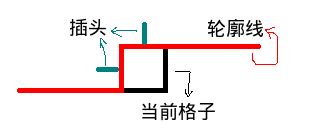
万年神坑插头DP，插头DP可以解决棋盘上的一些连通性问题（比如这题）。插头指的是一个格子与周围格子的连通情况，插头DP通过记录轮廓线上的插头状态来进行转移。

因为转移时轮廓线上只有两个位置的状态改变了，所以我们只需要关注这两个位置：

由于可以用若干条哈密顿回路，观察之后我们发现只需要知道这两个位置上是否连有插头即可，就可以进行转移：

1. A有插头，B有插头：当前格子一定有上插头和左插头，否则连不起来。
2. A有插头，B没有插头：当前格子一定有左插头，还可以有右插头或下插头（取决于右边或者下面是不是障碍，且不能同时有右插头和下插头），不能有上插头。
3. A没有插头，B有插头：当前格子一定有上插头，还可以有右插头或下插头（取决与右边或者下面是不是障碍，且不能同时有右插头和下插头），不能有左插头。
4. A没有插头，B没有插头：当前格子一定有右插头和下插头，因为每个格子都有两个插头。

还有障碍格子的转移问题，因为障碍格子不能连进来也不能连出去，所以直接传递就行了。

示例程序

#include<cstdio>
using namespace std;
typedef long long LL;
const int maxn=11,maxs=1<<maxn+1;

int te,n,m,pic[maxn+5][maxn+5];LL f[2][maxn+5][maxs];

int main(){
    freopen("program.in","r",stdin);freopen("program.out","w",stdout);
    for (int t=(scanf("%d",&te),1);t<=te;t++){
        scanf("%d%d",&n,&m);for (int i=1;i<=n;i++) for (int j=1;j<=m;j++) scanf("%d",&pic[i][j]);
        for (int s=0;s<(1<<m+1);s++) f[0][m][s]=0;f[0][m][0]=1;
        for (int i=1,c=1;i<=n;i++,c^=1){
            for (int j=0;j<=m;j++) for (int s=0;s<(1<<m+1);s++) f[c][j][s]=0;
            for (int s=0;s<(1<<m+1);s++) if (f[c^1][m][s]) f[c][0][s<<1]=f[c^1][m][s];
            for (int j=1;j<=m;j++)
                for (int s=0;s<(1<<m+1);s++){
                    LL F=f[c][j-1][s];bool A=s>>j-1&1,B=s>>j&1;
                    if (!pic[i][j]) {if (!A&&!B) f[c][j][s]+=F;}
                    else if (A&&B) f[c][j][s^(1<<j-1)^(1<<j)]+=F;
                    else if (A&&!B){
                        if (pic[i][j+1]) f[c][j][s^(1<<j-1)^(1<<j)]+=F;
                        if (pic[i+1][j]) f[c][j][s]+=F;
                    } else if (!A&&B){
                        if (pic[i][j+1]) f[c][j][s]+=F;
                        if (pic[i+1][j]) f[c][j][s^(1<<j-1)^(1<<j)]+=F;
                    } else if (pic[i][j+1]&&pic[i+1][j]) f[c][j][s^(1<<j-1)^(1<<j)]+=F;
                }
        }
        printf("Case %d: There are %lld ways to eat the trees.\n",t,f[n&1][m][0]);
    }
    return 0;
}