题目概述

有 $n$ 个点 $m$ 条单向边，每个点的不平衡度为出度减入度的差的绝对值，现在可以删除至多 $m-K$ 条边，求最大不平衡度的最小值。

解题报告

其实不难吧……只是水平限制了我的想象力……首先二分答案 $D$ ，令 $d_i$ 表示 $i$ 点的入度 $-$ 出度，对于一条单向边 $(x,y)$ 我们连 $x\to y$ 上界为 $1$ 的边，如果 $(x,y)$ 满载说明这条边被删。然后对于 $d_i$ 分类讨论一下：

1. $d_i\ge D$ ，那么至少要减掉 $d_i-D$ 的出度，所以连 $i\to T$ 下界为 $d_i-D$ 的边，但是又不能减爆，所以上界为 $d_i+D$ 。
2. $-D<d_i<D$ ，可加可减，连 $S\to i$ 上界为 $D-d_i$ ，连 $i\to T$ 上界为 $d_i+D$ 的边。
3. $d_i\le -D$ ，连 $S\to i$ 下界为 $-D-d_i$ ，上界为 $D-d_i$ 的边。

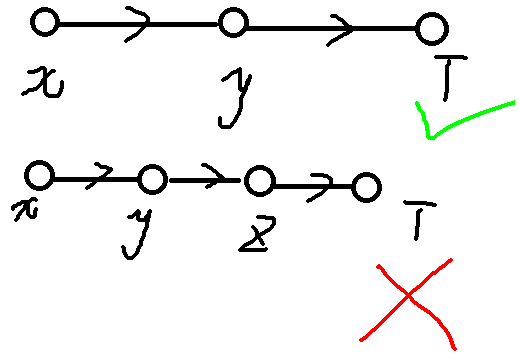
原本我以为直接刷上下界最小流就行了，然后疯狂WA，之后发现这样会出现一种违规的情况：

你看下面那种 $x$ 通过 $y$ 间接向 $z$ 提供流了啊，这并不符合我们的要求啊QAQ！！！

所以我们再引入费用，对于单向边 $(x,y)$ 连上界为 $1$ 费用为 $1$ 的边，其他边的费用为 $0$ 。这样的话显然会采取上面那种方法，从而防止下面错误的方法出现。

上下界费用流？我不会啊！其实就和上下界网络流一样……只不过换成了费用流……

示例程序

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<string>
#include<map>
#define fr first
#define sc second
#define mp make_pair
using namespace std;
const int maxn=52,maxm=maxn*maxn,maxe=(maxm+2*maxn)<<1,INF=2e9;

int te,n,S,T,SS,TT,m,K,x[maxm+5],y[maxm+5],d[maxn+5],num[maxn+5];
int E,lnk[maxn+5],son[maxe+5],nxt[maxe+5],w[maxe+5];
int que[maxn+5],ti,vis[maxn+5],dis[maxn+5],MIN[maxn+5];
pair<int,int> e[maxe+5];map<string,int> ID;

inline void Add(int x,int y,int L,int R,int c){
    son[E]=y;w[E]=c;e[E]=mp(0,R-L);nxt[E]=lnk[x];lnk[x]=E++;
        son[E]=x;w[E]=-c;e[E]=mp(0,0);nxt[E]=lnk[y];lnk[y]=E++;
    num[x]-=L;num[y]+=L;
}
#define AM(x) ((x)<maxn?((x)+1):0)
inline bool Spfa(int s,int t,int &MC,int &MF){
    static int fa[maxn+5],pre[maxn+5];memset(dis,63,sizeof(dis));MIN[t]=INF;
    int Head=0,Tail=0;que[++Tail]=s;vis[s]=++ti;dis[s]=0;MIN[s]=INF;
    while (Head!=Tail){
        int x=que[Head=AM(Head)];vis[x]=0;
        for (int j=lnk[x],u;~j;j=nxt[j])
            if (e[j].fr<e[j].sc&&dis[x]+w[j]<dis[u=son[j]]){
                dis[u]=dis[x]+w[j];MIN[u]=min(MIN[x],e[j].sc-e[j].fr);
                fa[u]=x;pre[u]=j;if (vis[u]<ti) que[Tail=AM(Tail)]=u,vis[u]=ti;
            }
    }
    if (MIN[t]==INF) return false;
    for (int x=t,j=pre[x];x!=s;x=fa[x],j=pre[x])
        e[j].fr+=MIN[t],e[j^1].fr-=MIN[t];
    return MC+=dis[t]*MIN[t],MF+=MIN[t],true;
}
inline int MCMF(int s,int t,int &MC) {int MF=0;while (Spfa(s,t,MC,MF));return MF;}
inline bool check(int D){
    E=0;memset(lnk,255,sizeof(lnk));memset(num,0,sizeof(num));
    int ful=0;for (int i=1;i<=m;i++) Add(x[i],y[i],0,1,1);
    for (int i=1;i<=n;i++)
        if (d[i]>=D) Add(i,T,d[i]-D,d[i]+D,0);
        else if (d[i]<=-D) Add(S,i,-d[i]-D,-d[i]+D,0);
        else Add(S,i,0,D-d[i],0),Add(i,T,0,d[i]+D,0);
    for (int i=S;i<=T;i++)
        if (num[i]>0) Add(SS,i,0,num[i],0),ful+=num[i];
        else if (num[i]<0) Add(i,TT,0,-num[i],0);
    Add(T,S,0,INF,0);int ans=0,MAX=0;if (MCMF(SS,TT,ans)<ful) return false;
    for (int j=lnk[SS];~j;j=nxt[j]) e[j].fr=e[j].sc,e[j^1].fr=e[j^1].sc;
    for (int j=lnk[TT];~j;j=nxt[j]) e[j].fr=e[j].sc,e[j^1].fr=e[j^1].sc;
    e[E-1].fr=e[E-1].sc;e[E-2].fr=e[E-2].sc;return MCMF(T,S,MAX),ans-MAX<=K;
}
int main(){
    freopen("program.in","r",stdin);
    freopen("program.out","w",stdout);
    for (int t=(scanf("%d",&te),1);t<=te;t++){
        scanf("%d%d%d",&n,&m,&K);K=m-K;memset(d,0,sizeof(d));ID.clear();
        S=0;T=n+1;SS=T+1;TT=SS+1;int tot=0;char s[25];string now;
        for (int i=1;i<=m;i++){
            scanf("%s",s);d[x[i]=ID.count(now=string(s))?ID[now]:ID[now]=++tot]--;
            scanf("%s",s);d[y[i]=ID.count(now=string(s))?ID[now]:ID[now]=++tot]++;
        }
        int L=0,R=n,mid;while (L<=R) check(mid=L+(R-L>>1))?R=mid-1:L=mid+1;
        printf("Case #%d:\n%d\n",t,L);
    }
    return 0;
}