题目概述

Jobs (Hard Version)

解题报告

首先我们先考虑二维不重复数点问题：

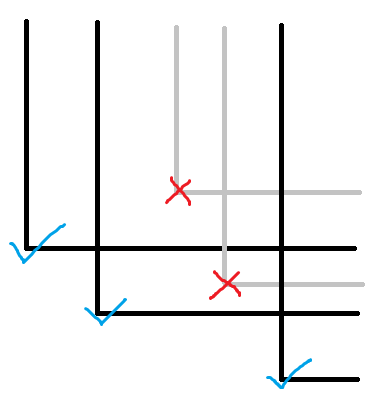
不难发现按照 $x$ 排序后，只有 $y$ 递降的那些点是有用的，其他点肯定都被包含在了某些点中。假设前一个点为 $(x_1,y_1)$ ，后一个点为 $(x_2,y_2)$ ，那么可以在 $(x_1,y_1)$ 标记 $1$ ，$(x_2,y_1)$ 标记 $-1$ ，最后做一遍二位前缀和，这样就可以避免重复计数。

考虑扩展到三维，按照 $x$ 递增的顺序考虑 $(y,z)$ 。对于 $x$ ，如果没有新的 $(y,z)$ ，那么 $x$ 当前的二维局面和 $x-1$ 是一致的，我们可以延续过来。但是如果需要新添加 $(y,z)$ ，在 $(y,z)$ 右上角的点都会被删除。因此考虑用set维护二维局面，当加入和删除点时，由于与上一个局面不同，因此我们需要在这些位置打上 $+1$ 或 $-1$ 标记来修正。最后做一次三维前缀和就可以得到答案。

为了方便，建议刚开始向set中添加左上角点 $(0,MAX+1)$ 以及右下角点 $(MAX+1,0)$ 。

示例程序

#include<set>
#include<cstdio>
#include<cctype>
#include<random>
#include<algorithm>
#define fr first
#define sc second
#define mp make_pair
#define A first
#define B second.first
#define C second.second
using namespace std;
typedef long long LL;
const int maxn=1000000,maxq=2000000,maxm=1000000,maxa=400,MOD=998244353;

int n,Q,seed,f[maxa+5][maxa+5][maxa+5],ans[maxq+5];
int m;pair<int, pair<int,int> > a[maxm+5];
set< pair<int,int> > S;set< pair<int,int> >::iterator it;

#define EOLN(x) ((x)==10 || (x)==13 || (x)==EOF)
inline char readc(){
    static char buf[100000],*l=buf,*r=buf;
    return l==r && (r=(l=buf)+fread(buf,1,100000,stdin),l==r)?EOF:*l++;
}
template<typename T> int readi(T &x){
    T tot=0;char ch=readc(),lst='+';
    while (!isdigit(ch)) {if (ch==EOF) return EOF;lst=ch;ch=readc();}
    while (isdigit(ch)) tot=(tot<<3)+(tot<<1)+(ch^48),ch=readc();
    lst=='-'?x=-tot:x=tot;return EOLN(ch);
}
inline void Update(int A,set< pair<int,int> >::iterator it,int x){
    f[A][it->fr][it->sc]+=x;
    f[A][next(it)->fr][it->sc]-=x;
}
inline int ADD(int x,int y) {return x+y>=MOD?x+y-MOD:x+y;}
inline int MUL(int x,int y) {return (LL)x*y%MOD;}
int main(){
    readi(n);readi(Q);
    for (int i=1;i<=n;i++){
        readi(m);
        for (int i=1;i<=m;i++) readi(a[i].A),readi(a[i].B),readi(a[i].C);
        sort(a+1,a+1+m);
        S.clear();S.insert(mp(0,maxa+1));S.insert(mp(maxa+1,0));
        for (int i=1;i<=m;i++){
            int A=a[i].A;pair<int,int> p=a[i].sc;
            it=prev(S.upper_bound(p));
            if (it->sc<=p.sc) continue;
            Update(A,it,-1);
            for (it++;it->sc>=p.sc;it=S.erase(it)) Update(A,it,-1);
            it=S.insert(p).fr;
            Update(A,it,1);Update(A,--it,1);
        }
    }
    for (int i=1;i<=maxa;i++)
        for (int j=1;j<=maxa;j++)
            for (int k=1;k<=maxa;k++)
                f[i][j][k]+=f[i-1][j][k];
    for (int i=1;i<=maxa;i++)
        for (int j=1;j<=maxa;j++)
            for (int k=1;k<=maxa;k++)
                f[i][j][k]+=f[i][j-1][k];
    for (int i=1;i<=maxa;i++)
        for (int j=1;j<=maxa;j++)
            for (int k=1;k<=maxa;k++)
                f[i][j][k]+=f[i][j][k-1];
    readi(seed);
    std::mt19937 rng(seed);
    std::uniform_int_distribution<> u(1,400);
    int lastans=0;
    for (int i=1;i<=Q;i++){
        int IQ=(u(rng)^lastans)%400+1;  // The IQ of the i-th friend
        int EQ=(u(rng)^lastans)%400+1;  // The EQ of the i-th friend
        int AQ=(u(rng)^lastans)%400+1;  // The AQ of the i-th friend
        lastans=f[IQ][EQ][AQ];  // The answer to the i-th friend
        ans[i]=lastans;
    }
    seed%=MOD;
    int pw=1,ha=0;
    for (int i=Q;i;i--){
        ha=ADD(ha,MUL(ans[i],pw));
        pw=MUL(pw,seed);
    }
    printf("%d\n",ha);
    return 0;
}