题目概述

CF1444D

解题报告

这题演我啊，我看三个 $1000$ 以为有什么高级的分半算法，结果写背包能过QAQ。

首先显然 $h\not=v$ 时无解，然后我们需要把水平线段和竖直线段都拆成两半，两半的和相等，作为 左/右 和 上/下。

分半用背包就可以解决，接下来我们考虑构造。由于线段不能相交，我们联想到凸多边形，因为凸多边形一定不会有两边相交。因此，一种可行的思路是想办法把线段搞成上凸壳和下凸壳。

上凸壳，即斜率递减，只要让水平线段逐渐增大，竖直线段逐渐减小就可以构造出来。同理下凸壳只要让水平线段逐渐减小，竖直线段逐渐增大。

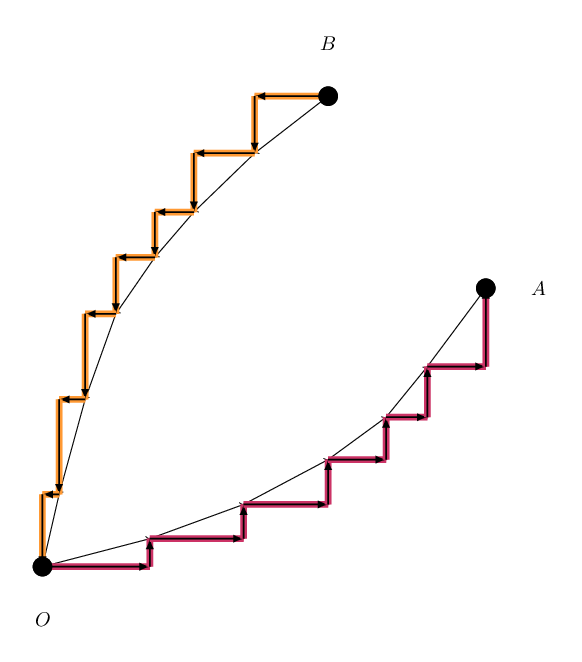
这么处理我们就能得到这样的图形（图是盗的）：

然后只要用剩下的线段把 $A$ 点 $B$ 点连起来就行了（顺序随意）。

为了避免讨论，我们可以强制水平线段少的部分（ $\le {n\over 2}$ 个）放在前面，竖直线段多的部分（ $\ge {n\over 2}$ ）放在前面，这样就分为了三组（一组上凸壳，一组下凸壳，一组剩余的）。

示例程序

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn=1000,maxt=maxn*maxn;

int te,n,a[maxn+5],m,b[maxn+5],f[maxt+5],c[maxn+5],ti,vis[maxn+5];

bool Make(int *a,bool fl){
    int C=0;for (int i=1;i<=n;i++) C+=a[i];
    if (C&1) return false;C>>=1; 
    f[0]=true;for (int i=1;i<=C;i++) f[i]=0;
    for (int i=1;i<=n;i++)
        for (int j=C;j>=a[i];j--)
            if (!f[j] && f[j-a[i]]) f[j]=i;
    if (!f[C]) return false;
    c[0]=0;ti++;for (int x=C;x;x-=a[f[x]]) c[++c[0]]=a[f[x]],vis[f[x]]=ti;
    int cnt=c[0];for (int i=1;i<=n;i++) if (vis[i]<ti) c[++c[0]]=a[i];
    if ((cnt<=(n>>1))^fl){
        int j=0;
        for (int i=1;i<=cnt;i++) a[++j]=c[i];
        for (int i=cnt+1;i<=n;i++) a[++j]=c[i];
        a[0]=cnt;
    } else {
        int j=0;
        for (int i=cnt+1;i<=n;i++) a[++j]=c[i];
        for (int i=1;i<=cnt;i++) a[++j]=c[i];
        a[0]=n-cnt;
    }
    return true;
}
inline bool cmp(const int &a,const int &b) {return a>b;}
int main(){
    for (scanf("%d",&te);te;te--){
        scanf("%d",&n);for (int i=1;i<=n;i++) scanf("%d",&a[i]);
        scanf("%d",&m);for (int i=1;i<=m;i++) scanf("%d",&b[i]);
        if (n!=m || !Make(a,0) || !Make(b,1)) {puts("No");continue;}
        sort(a+1,a+a[0]+1,cmp);sort(a+a[0]+1,a+n+1,cmp);
        sort(b+1,b+b[0]+1);sort(b+b[0]+1,b+n+1);
        puts("Yes");int x=0,y=0;
        for (int i=1;i<=a[0];i++) printf("%d %d\n",x+=a[i],y),printf("%d %d\n",x,y+=b[i]);
        for (int i=a[0]+1;i<=b[0];i++) printf("%d %d\n",x-=a[i],y),printf("%d %d\n",x,y+=b[i]);
        for (int i=b[0]+1;i<=n;i++) printf("%d %d\n",x-=a[i],y),printf("%d %d\n",x,y-=b[i]);
    }
    return 0;
}