题目概述

给出一个数组，求这个数组的 $k$ 次前缀和（前缀和的前缀和的前缀和……）。

解题报告

可能大力找规律就可以很快做出来？

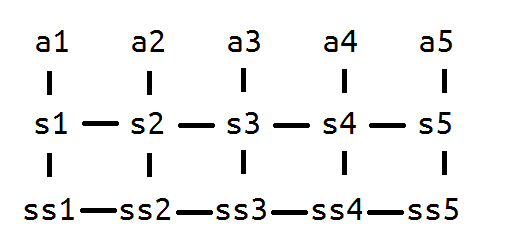
不过我们可以考虑这个东西的组合意义，$a_i$ 对 $k$ 次前缀和中的第 $j$ 项 $s_{k,j}$ 的贡献其实就是 $(0,i)$ 走到 $(k,j)$ 的方案数（必须先往下走一次）：（图By AntiQuality）

所以 $s_{k,j}=\sum_{i=1}^{j}a_i{j-i+K-1\choose j-i}$ 。

示例程序

#include<cstdio>
using namespace std;
typedef long long LL;
const int maxn=2000,MOD=1e9+7;

int n,K,a[maxn+5],c[maxn+5],INV[maxn+5],ans[maxn+5];

inline int C(int x,int y) {int ans=INV[y];for (int i=1;i<=y;i++) ans=(LL)ans*(x-i+1)%MOD;return ans;}
inline void Make(int n){
    INV[0]=INV[1]=1;for (int i=2;i<=n;i++) INV[i]=(LL)(MOD-MOD/i)*INV[MOD%i]%MOD;
    for (int i=1;i<=n;i++) INV[i]=(LL)INV[i-1]*INV[i]%MOD;for (int i=0;i<=n;i++) c[i]=C(i+K-1,i);
}
inline void AMOD(int &x,int tem) {if ((x+=tem)>=MOD) x-=MOD;}
int main(){
    freopen("program.in","r",stdin);freopen("program.out","w",stdout);
    scanf("%d%d",&n,&K);for (int i=1;i<=n;i++) scanf("%d",&a[i]);
    if (!K) {for (int i=1;i<=n;i++) i<n?printf("%d ",a[i]):printf("%d\n",a[i]);return 0;}
    Make(n);for (int i=1;i<=n;i++) for (int j=i;j<=n;j++) AMOD(ans[j],(LL)a[i]*c[j-i]%MOD);
    for (int i=1;i<=n;i++) i<n?printf("%d ",ans[i]):printf("%d\n",ans[i]);return 0;
}