题目概述

给出 $n$ 个带权点和 $m$ 条无向边的图，给出 $q$ 个操作：1.修改某个节点的点权。2.询问 $x\to y$ 路径上所有简单路径的最小点权。

解题报告

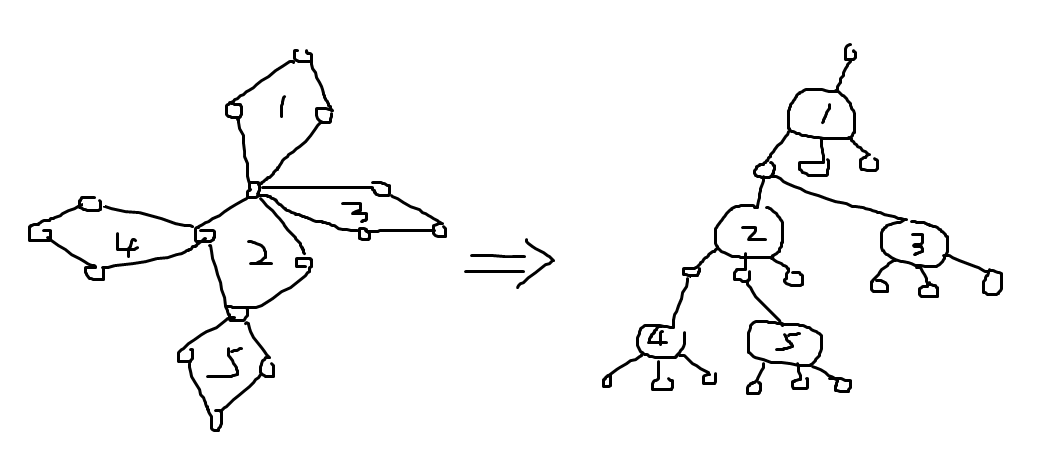
简单路径就是一个点不能重复经过，所以想到点双中的点合并。但是一个点可以在多个点双中（割点），这就要借助圆方树来处理。来看看灵魂画师Manchery生动形象的图：

大概就是在割点和点双中的点之间加上一个方点（图中的大点），然后把点双中的点都连向方点，这样问题就转变到了树上，用树链剖分+线段树就可以搞啦。至于修改点权，用multiset维护每个方点就行了。

要注意的是，如果两个点的祖先是方点，那么还需要算上方点的父亲（割点），当然如果祖先不是方点就直接算上贡献。

示例程序

写到神志不清，multiset竟然开成了set，成功爆炸。

#include<cstdio>
#include<cctype>
#include<cstring>
#include<algorithm>
#include<set>
using namespace std;
const int maxn=200000,maxm=200000;

int K,n,m,te,a[maxn+5],ti,dfn[maxn+5],low[maxn+5],tp,stk[maxn+5];
int E,lnk[2][maxn+5],nxt[(maxm<<1)+5],son[(maxn<<1)+5];
multiset<int> S[maxn+5];multiset<int>::iterator it;int MIN[(maxn<<2)+5];
int fa[maxn+5],dep[maxn+5],si[maxn+5],Lt[maxn+5],who[maxn+5],SH[maxn+5],top[maxn+5];

#define Add(ID,x,y) (son[E]=(y),nxt[E]=lnk[ID][x],lnk[ID][x]=E++)
void Tarjan(int x,int pre=-1){
    dfn[x]=low[x]=++ti;stk[++tp]=x;
    for (int j=lnk[0][x],u;~j;j=nxt[j])
        if ((j^1)!=pre) if (!dfn[u=son[j]]){
                Tarjan(u,j);low[x]=min(low[x],low[u]);
                if (low[u]>=dfn[x])
                    for (int y=(n++,Add(1,x,n),stk[tp--]);;y=stk[tp--])
                        {Add(1,n,y);S[n].insert(a[y]);if (y==u) break;}
            } else low[x]=min(low[x],dfn[u]);
}
void Dfs(int x,int pre=0){
    fa[x]=pre;dep[x]=dep[pre]+1;si[x]=1;
    for (int j=lnk[1][x];~j;j=nxt[j]) Dfs(son[j],x),si[x]+=si[son[j]],si[son[j]]>si[SH[x]]?SH[x]=son[j]:0;
}
void HLD(int x,int lst=0){
    who[Lt[x]=++ti]=x;top[x]=lst;if (SH[x]) HLD(SH[x],lst);
    for (int j=lnk[1][x];~j;j=nxt[j]) if (son[j]!=SH[x]) HLD(son[j],son[j]);
}
#define val(x) (S[x].begin()==S[x].end()?(int)2e9:*S[x].begin())
#define Pushup(p) (MIN[p]=min(MIN[(p)<<1],MIN[(p)<<1|1]))
void Build(int l,int r,int p=1){
    if (l==r) {MIN[p]=val(who[l]);return;}int mid=l+(r-l>>1);
    Build(l,mid,p<<1);Build(mid+1,r,p<<1|1);Pushup(p);
}
void Update(int x,int l=1,int r=n,int p=1){
    if (l==r) {MIN[p]=val(x);return;}int mid=l+(r-l>>1);
    if (Lt[x]<=mid) Update(x,l,mid,p<<1); else Update(x,mid+1,r,p<<1|1);Pushup(p);
}
int Query(int L,int R,int l=1,int r=n,int p=1){
    if (R<l||r<L) return 2e9;if (L<=l&&r<=R) return MIN[p];int mid=l+(r-l>>1);
    return min(Query(L,R,l,mid,p<<1),Query(L,R,mid+1,r,p<<1|1));
}
inline int Ask(int x,int y,int MIN=2e9){
    while (top[x]!=top[y]){
        if (dep[top[x]]<dep[top[y]]) swap(x,y);
        MIN=min(MIN,Query(Lt[top[x]],Lt[x]));x=fa[top[x]];
    }
    if (Lt[x]>Lt[y]) swap(x,y);MIN=min(MIN,Query(Lt[x],Lt[y]));
    if (x>K) MIN=min(MIN,a[fa[x]]); else MIN=min(MIN,a[x]);return MIN;
}
#define Change(x,y) (it=S[fa[x]].find(a[x]),S[fa[x]].erase(it),S[fa[x]].insert(a[x]=(y)))
int main(){
    freopen("program.in","r",stdin);freopen("program.out","w",stdout);
    scanf("%d%d%d",&n,&m,&te);K=n;memset(lnk,255,sizeof(lnk));
    for (int i=1;i<=K;i++) scanf("%d",&a[i]);
    for (int i=1,x,y;i<=m;i++) scanf("%d%d",&x,&y),Add(0,x,y),Add(0,y,x);
    for (int i=1;i<=K;i++) if (!dfn[i]) Tarjan(i);ti=0;
    for (Dfs(1),HLD(1),Build(1,n);te;te--){
        char ch=getchar();while (ch!='A'&&ch!='C') ch=getchar();int x,y;scanf("%d%d",&x,&y);
        if (ch=='A') printf("%d\n",Ask(x,y)); else if (fa[x]) Change(x,y),Update(fa[x]); else a[x]=y;
    }
    return 0;
}